Boy oh boy, the next installment in the epic saga of inequalities is finally here! How wonderful.
A while ago, one of my friends gave me this inequality, and, being the analysis enthusiast that I am, I couldn't resist using partial derivatives to solve it. Even though I found a solution, I feel a bit unfulfilled; I used Desmos to find the roots of a polynomial, and that wouldn't be allowed during a contest. Fortunately, this blog isn't a Maths contest, so it shall be allowed here. I suppose there were other methods of finding the roots of the polynomial I'm talking about, but they probably involved a lot of calculations that I wouldn't have had the patience to go through.
Let \(x,y,z\) be real, strictly positive numbers satisfying \(xyz=1\). Prove that \((x^{10}+y^{10}+z^{10})^2\) is bigger or equal to \(3(x^{13}+y^{13}+z^{13})\).
Solution:
Let \(f(x,y,z)=(x^{10}+y^{10}+z^{10})^2-3(x^{13}+y^{13}+z^{13})\) and \(g(x,y,z)=xyz\). We know that, in order to reach the extremes, $$∇f(x,y,z)=λ∇g(x,y,z) ⇒\frac{𝛛f}{𝛛x}=λ\frac{𝛛g}{𝛛x}$$The same relation works for \(y\) and \(z\). By differentiating, we get that $$20x^9(x^{10}+y^{10}+z^{10})-39x^{12}=λyz$$
$$⇒ 20x^{10}(x^{10}+y^{10}+z^{10})-39x^{13}=λ$$because \(xyz=1\). Thus, we get, by multiplying with \(y^{10}\), that $$20x^{10}y^{10}(x^{10}+y^{10}+z^{10})-39x^{13}y^{10}=λy^{10}$$
By doing the same for \(y\) and subtracting the two relations, we get that $$λ(y^{10}-x^{10})=39x^{10}y^{10}(y^3-x^3)$$and, by dividing the whole thing by \(x^{10}y^{10}\), which we can, since the numbers are strictly positive, we get that $$λ(x^{-10}-y^{-10})=39(y^3-x^3)$$This implies that $$λx^{-10}+39x^3=λy^{-10}+39y^3=λz^{-10}+39z^3$$since the relation is symmetrical. With that in mind, let \(h(x)=λx^{-10}+39x^3\). By differentiating this function, we get the derivative being equal to \(\frac {dh}{dx}=-10λx^{-11}+117x^2\).
Let us now prove that \(λ>0\). For this, we shall presume that \(x≤y≤z\), so that \(x≤1\), and look at \(20x^{10}(x^{10}+y^{10}+z^{10})-39x^{13}≥20x^{10}(x^{10}+2x^{-5})-39x^{13}=20x^{20}+40x^{5}-39x^{13}≥0\), with the first part coming from the AM-GM inequality and the second coming from the fact that \(x\) is smaller than 1. Thus, \(λ\) is positive.
Back to the derivative of \(h\), since \(λ\) is positive, we get that there is only one value of \(x\) for which the derivative is 0, and, thus, there are at most 2 points with the same output of the function. Thus, either \(x=y=z=1\), or \(x=y,z=x^{-2}\). In the latter case, we shall go back to \(\frac{𝛛f}{𝛛x}=λ\frac{𝛛g}{𝛛x}\) and \(\frac{𝛛f}{𝛛z}=λ\frac{𝛛g}{𝛛z}\) subtract the derivatives and multiply by \(x^{40}\) in order to obtain that \(40x^{60}-39x^{53}-20x^{30}+39x^{14}-20=0\). This is the part where I used Desmos.
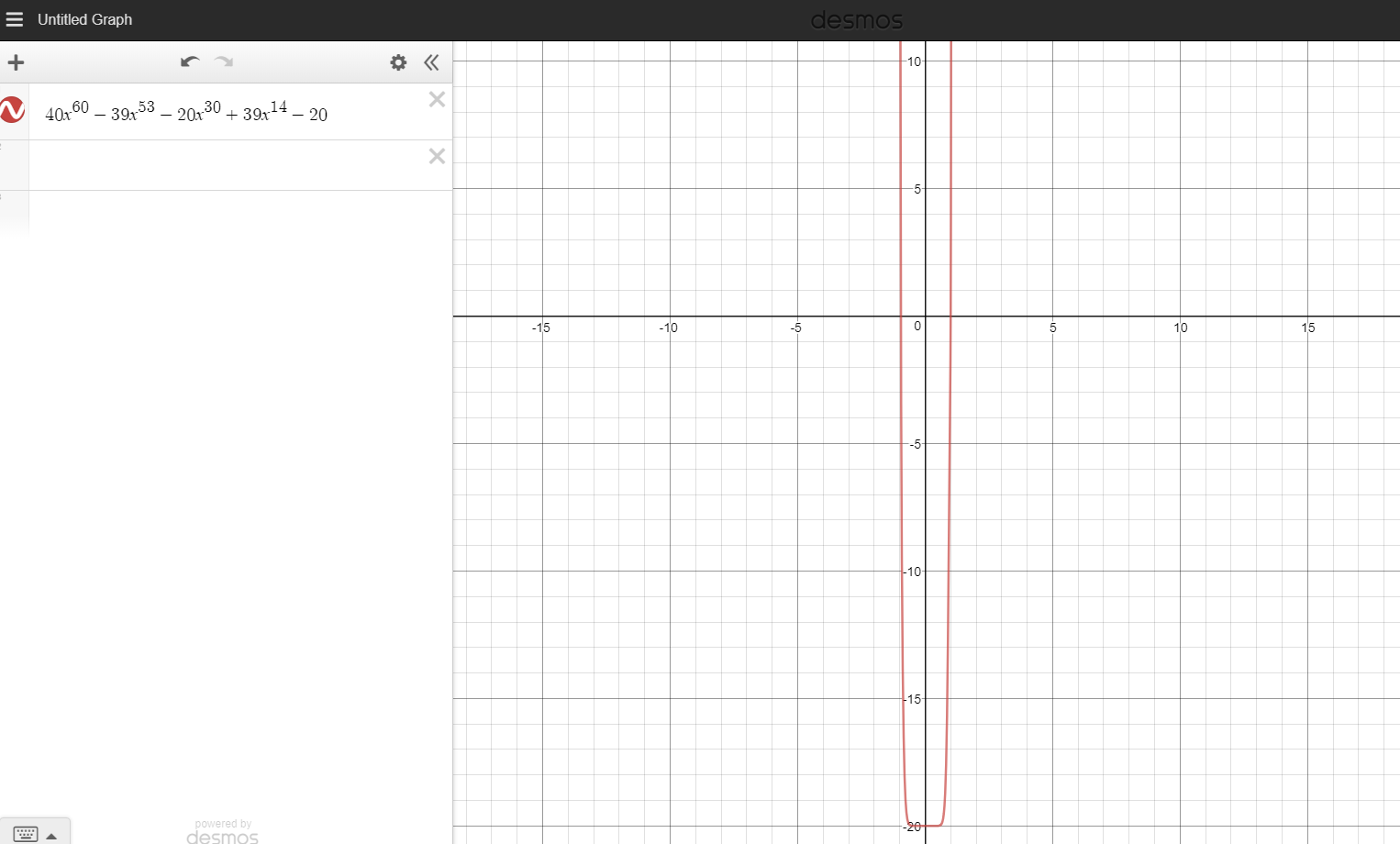
As you can see, the only real root of the polynomial is 1, so this means that \(x=y=z=1\) yet again. It's obvious that \(f(1,1,1)=0\), but now we have to prove that this is the minimal value, because we wanted to prove that \(f(x,y,z)≥0\) when \(g(x,y,z)=1\). Since this is a global extreme, we only have to find a triplet \(x,y,z\) for which the conditions apply. By taking \(z\) very large, towards infinity, and with \(x\) and \(y\) taken accordingly, we obtain an \(f\) that approaches infinity, and, thus, is bigger than 0. This concludes the proof.
Perhaps I should have tried finding the roots of that polynomial without computer help. I am not sure how I could have done it, but I asked one of the teachers at Oxford during the interview about that and he suggested a method of approximating the roots. Even so, calculating the roots without Desmos would have taken a really long while to write, and I am forever thankful to computers. I really liked this inequality, it really tests the solver's capacity of manipulating functions...and graphing applications. Tune in next time for a combinatorics problem taken from a college contest, or something completely random!
Cris.
No comments:
Post a Comment