Earth's escape velocity
You'd be surprised how many intriguing Physics results are on the borderline between high school Maths and College Maths. This one is one of my favorites, mainly because it is actually applied (probably) in rocket science and it gives the feeling of greatness to anyone calculating/understanding it.
Before we start, let me give you some formulas:
The force of attraction between two bodies of masses M and m respectively, with a distance R between their center of masses, is $$F=\frac{GMm}{R^2}$$ (I actually managed to properly write fractions!)
G is the constant of gravitation, which is roughly equal to \(6.7*10^{-11} Nkg^{-2}m^2\). The mass of the Earth is \(5.972*10^{24}kg\), but, to make the job of the calculator easier, we shall use \(6*10^{24}kg\). The radius of the Earth is \(6,4*10^{6}m\). Now that we know these formulas, we can get to the task at hand.
The net force required to leave the Earth is, obviously, equal to the attraction force. Because an object is incredibly small compared to the radius of a planet, we shall consider the distance between the object and planet equal to the radius of the planet.
In order to leave the planet, one must exert work with distance reaching infinity, and, thus, the work needed to escape the planet is $$\int_R^⧞ \frac {MmG}{R^2} dr=\frac {MmG}{R}=\frac{mv^2}{2}$$.
Thus, we get that \(v^2=\frac {2MG}{R}\), so \(v={(2MG)^{1/2}}{R^{1/2}}\). By plugging in the mentioned constants, we get that the speed is about 11.20825 kilometers per second. That's roughly 40338 kilometers per hour.
You'd think that such a speed can be achieved only by incredibly complex pieces of technology with highly complex engines and complicated patterns, yet the first object to reach escape velocity is a steel plate covering a nuclear test back in 1957. It is unknown if it did actually leave Earth's atmosphere, as it would have probably boiled due to the high speed, but one thing is sure: no one found its debris. Who knows, maybe the first man-made creation the aliens find won't be one of the Voyager probes, but rather a random steel plate floating randomly through the Solar System.
Cris.
Old Topology Problem
'Gazeta Matematica', the most widely known Mathematical journal in Romania, begins its year by publishing problems from old years ending in the same digit as the year that just started. This year, they published problems from years ending in 8. The problem that I am about to share was published in 1968 by T. Zamfirescu, and is solvable through Helly's theorem. Without further ado, let's get straight into the problem.
Let d be a line in space and S a finite set of spheres such that any 3 spheres have an interior point in common. Prove that there exists a line d' parallel to d that intersects all the spheres.
Helly's theorem in a plane states that if a finite number of convex sets with the property that any three convex sets intersect, then all convex sets intersect.
Here's the proof of the theorem: Let m be smaller or equal to n, where m is the maximum number of sets with the intersection I different than the empty set and let us presume by absurd that \(m<n\), so there is C such that C doesn't intersect with I. Because C and I are convex sets, there must be a line d that separates them, they are in planes \(S_1\) and \(S_2\) respectively. Because \(m>2\), we need at least 3 sets to create I. Let \(C_1\) and \(C_2\) be two of them. Obviously, I is included in them. From the hypothesis, \(C_1\), \(C_2\) and C intersect. We choose the point A in their intersection and the point B in I. Thus, A is in \(S_1\) and B is in \(S_2\). Since A and B are in \(C_1\) and \(C_2\), the whole segment AB is in \(C_1\) and \(C_2\), and, thus, AB and d intersect. We now have that for any sets \(C_1\) and \(C_2\) that contain I, the intersection between \(C_1, C_2\) and d is not the empty set. By writing in a different form, we have that the intersection between \(C_1\) and d intersects with the intersection between $C_2$ and d. Thus, by considering the intersections as segments, we have m segments on a line such that each pair of segments intersects. By Helly's theorem on a line, we have that all the m segments intersect, so, by writing the intersection of the segments as the intersection of \(C_i\)-s and d, we have that I intersects with d, which is a contradiction. Thus, m=n.
Back to the problem at hand, let us consider a plane P such that d is perpendicular on P. Now, let us project the spheres on P. We get a set of circles with the property that any 3 of them intersect, and, thus, from Helly's theorem in a plane, we get that the circles intersect. Since the spheres intersect in an interior point, the circles have an actual surface in common, not only a point. Let A be a point in that surface. The line through A that is parallel to d is the required d'.
Of course, this problem isn't a hard topology problem, but it is pretty hard for the undergraduate level.
This article wasn't the different article that I promised. That one is still underway. Stay tuned folks, more problems/journals/randomness is coming.
Cris.
Matrix solvable through Jordan form
One of the worst experiences (and failures) of my life was the National Maths Olympiad from the 11th grade. It was a traumatizing experience, since the Olympiad took place in a remote part of the country (I come from Romania), and the subjects were incredibly hard. I managed to win a bronze medal, though I was very disappointed with myself. A month ago, I gathered my strength and looked through the shortlist for the Olympiad. The problem I am about to solve was the only linear algebra problem in the shortlist, and, just like the one from the Olympiad, it is solvable through the Jordan canonical form. The Jordan form wasn't part of the syllabus of the Olympiad, which was a dirty move from the problem selection committee. Nonetheless, I was inspired by this experience, and, in the meantime, I studied the canonical form.
Without further ado, let's get straight into the problem.


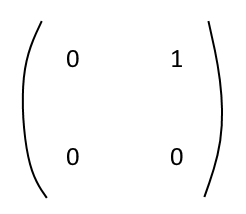
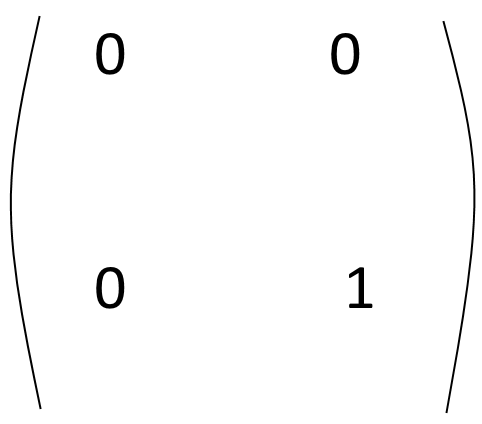
 ,
,  .
.
Let A be an \(n x n\) matrix with complex entries. Prove that \(A^2=O_{n}\) if and only if there are complex \(n x n\) matrices B and C such that \(A = BC\) and \(CB=O_{n}\).
I will post the matrices as photos, because posting them in Latex is tedious.
Let 1) be \(A^2=O_{n} => B, C\), and 2) be \(B, C => A^2=O_{n}\).
2) => 1)
$$A=BC, CB=O_{n}$$
$$A^2=B(CB)C=O_{n}$$
The next one will be 'slightly' longer.
1) => 2)
\(A^2=O_{n}\) Thus, the minimal polynomial of A divides \(X^2\).
1. The minimal polynomial of A is X, so \(A=O_{n}, B=O_{n}\), while C is any random matrix.
2. The minimal polynomial is \(X^2\)

We shall start using the Jordan canonical form. We know that the maximum order of any Jordan block corresponding to a specific eigenvalue is equal to the number of apparitions of \(X-a\) (where a is an eigenvalue) in the minimal polynomial. Thus, the maximum order of a Jordan cell is 2, and the Jordan canonical form of A looks something like this:

Everything above the J-s and 0-s is 0. The J-s look something like this:

We shall be looking for matrices B' and C' such that \(B' C' = J\) and \(C' B' = O_{n}\)
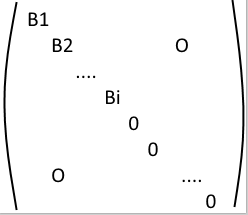
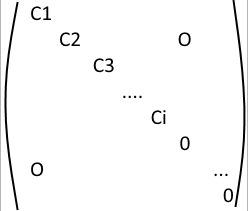
Let us write B' and C' in the form
 ,
,  .
.
We need to find \(B_{i}\) and \(C_{i}\) such that \(B_{i} C_{i} = J_{i}\) and $$C_{i} B_{i} = O_{n}$$. The perfect example of such matrices is \(B_{i}=J_{i}\) and \(C_{i}\) of the form

With \(B_{i}\) and \(C_{i}\) found, we can write B' and C'.
Let S be a matrix such that \(SAS^{-1} = J\). Thus, \(S^{-1}JS=A\), and \(S^{-1}B' C' S=A\). We can take \(B=S^{-1}B'\), and \(C=C'S\). Thus, \(BC=A\) and \(CB=C'SS^{-1}B'=C'B'=O_{n}\), so there exist B and C, which concludes the problem.
It was very interesting to solve a problem with the Jordan canonical form, as the methods used aren't very common in high school Mathematics. The problem itself wasn't extremely difficult, yet it was interesting nonetheless. Tune in next time for an article that might be about something rather...different.
Cris.
Gamer's Journal #2
Hello there! Today on our second release of Gamer's Journal I am going to present you the specs of the new Ray-Tracing Geforce RTX Lineup from NVidia , featuring the RTX 2070 , RTX 2080 , RTX 2080Ti .
Here you will find the specs of them , and the cost as well :
Geforce RTX 2070 FE Specs & Price :
-NVIDIA CUDA Cores : 2304
-RTX-OPS : 45T
-Giga Rays : 6
-Boost Clock [MHz]: 1710(OC)
-Base Clock [MHz]: 1410
-Standart Memory Config : 8GB GDDR6
-Memory Speed : 14 Gbps
-Memory Interface Width : 256-bit
-Memory Bandwidth : 448 GB/s
-Standard Display Connectors : DisplayPort , HDMI , USB Type-C ,DVI-DL
-Graphics Card Power [W] : 185W
-Supplementary Power Connectors : 8 pin
-Price : $ 599.00
Geforce RTX 2080 FE Specs & Price :
-NVIDIA CUDA Cores : 2944
-RTX-OPS : 60T
-Giga Rays : 8
-Boost Clock [MHz] : 1800(OC)
-Base Clock [MHz] : 1515
-Standart Memory Config : 8GB GDDR6
-Memory Speed : 14 Gbps
-Memory Interface Width : 256-bit
-Memory Bandwidth : 448 GB/s
-Standard Display Connectors : DisplayPort, HDMI, USB Type-C
-Graphics Card Power [W]: 225W
-Supplementary Power Connectors : 6 pin + 8 pin
-Price : $ 799.00
Geforce RTX 2080Ti FE Specs & Price :
-NVIDIA CUDA Cores : 4352
-RTX-OPS : 78T
-Giga Rays : 10
-Boost Clock [MHz] : 1635(OC)
-Base Clock [MHz] : 1350
-Standart Memory Config : 11 GB GDDR6
-Memory Speed : 14 Gbps
-Memory Interface Width : 352-bit
-Memory Bandwidth : 616 GB/s
-Standard Display Connectors : DisplayPort, HDMI, USB Type-C
-Graphics Card Power [W] : 260W
-Supplementary Power Connectors : 8 pin + 8 pin
-Price : $ 1,199.00
These GPUs are using Ray Tracing , which is a new technology ( and the definitive solution ) for lifelike lighting , reflections , and shadows , offering a level of realism far beyond what's possible using traditional rendering techniques .
These new Turing GPUs feature new advanced shading technologies that are more powerful, flexible, and effiecient than ever before. Combined with the world's fastest memory - GDDR6 - this performance lets your rip and tear through games with maxed-out settings and incrediibly high frame rates .
Note that they won't be compatible with current SLI Bridges , so you will have to buy the new Geforce RTX NVLink Bridge .
These specs are taken from NVidia's Official Site , so no scammerino
In the next Gamer's Journal , I am going to talk about a video game that combines 2 major industries : Gaming and PC Components ! Stay tuned to find out
-NVIDIA CUDA Cores : 4352
-RTX-OPS : 78T
-Giga Rays : 10
-Boost Clock [MHz] : 1635(OC)
-Base Clock [MHz] : 1350
-Standart Memory Config : 11 GB GDDR6
-Memory Speed : 14 Gbps
-Memory Interface Width : 352-bit
-Memory Bandwidth : 616 GB/s
-Standard Display Connectors : DisplayPort, HDMI, USB Type-C
-Graphics Card Power [W] : 260W
-Supplementary Power Connectors : 8 pin + 8 pin
-Price : $ 1,199.00
These GPUs are using Ray Tracing , which is a new technology ( and the definitive solution ) for lifelike lighting , reflections , and shadows , offering a level of realism far beyond what's possible using traditional rendering techniques .
These new Turing GPUs feature new advanced shading technologies that are more powerful, flexible, and effiecient than ever before. Combined with the world's fastest memory - GDDR6 - this performance lets your rip and tear through games with maxed-out settings and incrediibly high frame rates .
Note that they won't be compatible with current SLI Bridges , so you will have to buy the new Geforce RTX NVLink Bridge .
These specs are taken from NVidia's Official Site , so no scammerino
In the next Gamer's Journal , I am going to talk about a video game that combines 2 major industries : Gaming and PC Components ! Stay tuned to find out
Gamer's Journal #1
Here on Gamer's Journal , you are going to find info about new Computer Components , as well peripherials , but most importantly , info about new video games !
So , without further ado , let's get to the main info about your next PC upgrade! Intel gave us earlier this day an opportunity to preorder their new 9th gen Skylake-S CPU's .
Here are the specs of them :
Core i9-9900K : It is going to have 8 processing cores and 16 threads , it has a base clock of 3.6 GHz (It can be further overclocked up to 5.0 GHz on one or 2 cores) , and 16 MB of Intel Smart Cache . It draws about 95W from the PSU , and it comes at a cost of 450 USD .
Core i7-9700K : It is going to have the same number of cores as the i9 , but half the amount of threads . It has a base clock of 3.6 GHz , same as the core i9 (It can be further overclocked up to 4.9 GHz on 1 core) . It has 12 MB of Intel Smart Cache , and draws about 95W from the PSU , coming at a cost of no more than 350 USD .
Core i5-9600K : It is going to have 6 cores and 6 threads , and it is gonna have a base clock of 3.7 GHz (It can be further overclocked up to 4.6 GHz on 1 core) . It has 9 MB of Intel Smart Cache , and draws about 95W from the PSU . It comes at a reduced cost of about 100 USD than its 8th gen brother , being about 250 USD .
Keep in mind that these Skylake-S CPUs are compatible with curent Z370 Chipset Motherboards , but they can be fully operational on a new motherboard with a new Z390 Chipset .
Note that all the specs given above are official , so no scammerino
In the next Gamer's Journal , I am going to talk about NVidia's new Ray-Tracing RTX 2070 , 2080 , 2080Ti , so stay tuned !!
Signed by Papa Radu
Our newest member
The Science Blog is pleased to welcome our new member, Lightwall AKA Radu AKA my cousin! He is an enthusiast of anything technological, and he will write interesting articles regarding computers, while also coordinating the Gamer's Journal, which will contain info about all sorts of things that will surely benefit any gamer. He's also a pro gamer, his favorite games being DOOM, CoD and Rocket League. I hope you'll enjoy his articles!
Cris.
An interesting puzzle in probability (which has almost nothing to do with probability)
When I was younger, sometime during the 4th grade or so, I had this subject at school called 'Funny Mathematics' (quite informal for a school subject). I was quite intrigued by it during the summer before 4th grade, mainly because I had no idea what it would involve. I had high expectations from it, but was disappointed when the school year started and we got our manuals. After going through the 'Funny Mathematics' manual, I found out that it contained some sort of brain teasers ('If Mary's dad has 3 daughters, 2 of which are called May and August, what is the name of the 3rd one' and other variations of this question) and some puzzles with sticks (the typical 'move the sticks so that the resulting operation is correct' questions). Let me just say, I never found that type of Mathematics to be funny. However, earlier this year, I came across Martin Gardner's 'Colossal Book of Short Puzzles and Problems', which contained a lot of intriguing problems that reminded me that funny mathematics actually exists. One of them, proposed in the Probability chapter, goes as follows:
'A man arrives at a random spot several miles from the Pentagon. He looks at the building through binoculars. What is the probability that he will see three of its sides?'
The fact that he watches through binoculars implies that we don't have to deal with the limitation of eyesight; we can presume, for the sake of this problem, that the man can see the Pentagon from a point infinitely far from the Pentagon.
I will present two solutions, one trivial (the solution proposed in the book; sadly, I didn't think of it), and my solution, involving calculus.
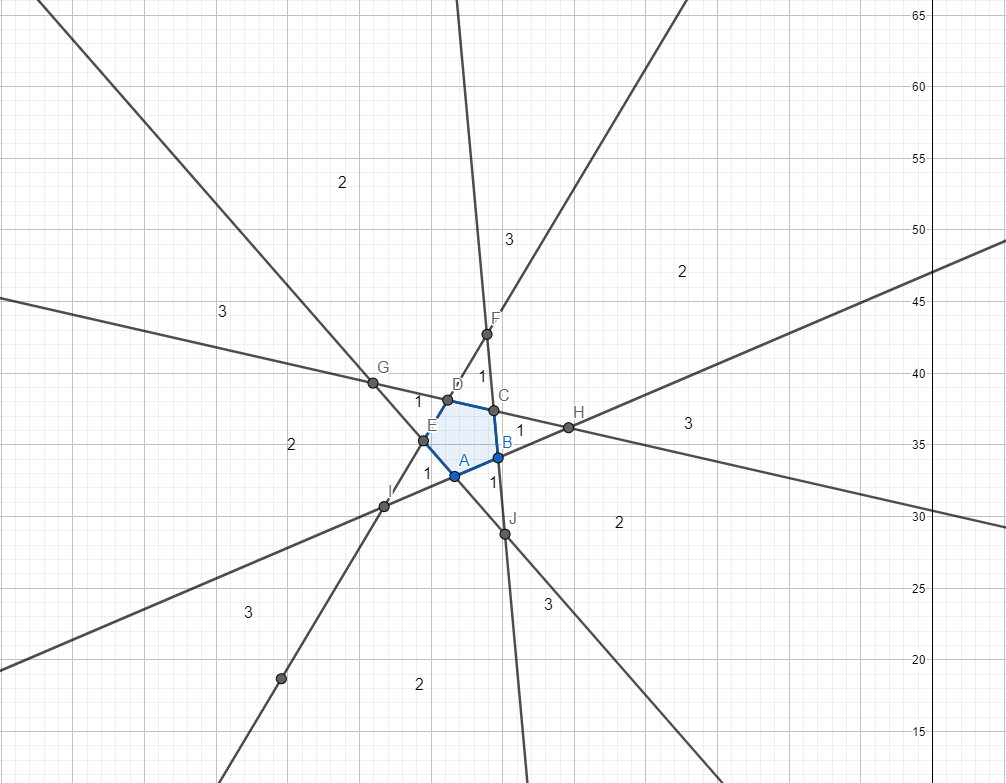
First solution:
Let us drawn the Pentagon and call it ABCDE. By intersecting the sides of the Pentagon, we can denote the areas in which the observer can see 1, 2 or 3 sides.
The drawing above shows the areas for which the observer sees 1, 2 and, respectively, 3 faces of the pentagon. Let us observe that, if the observer stays in a 2-area, then the symmetric of the observer through the center of the Pentagon, then the symmetric of the observer has an infinitely small chance of lying in the 1-area and a probability of being in a 3-area. Thus, the probability of the observer seeing 3 sides is the same as the probability of the observer seeing 2 sides, and the probability that the observer sees 1 side tends towards 0. Thus, \(P(1)+P(2)+P(3)=2P(3)=1\), so \(P(3)=1/2\).
Sadly, as I said, I couldn't see this solution when I solved the problem. Let me show you my solution.
Second solution:
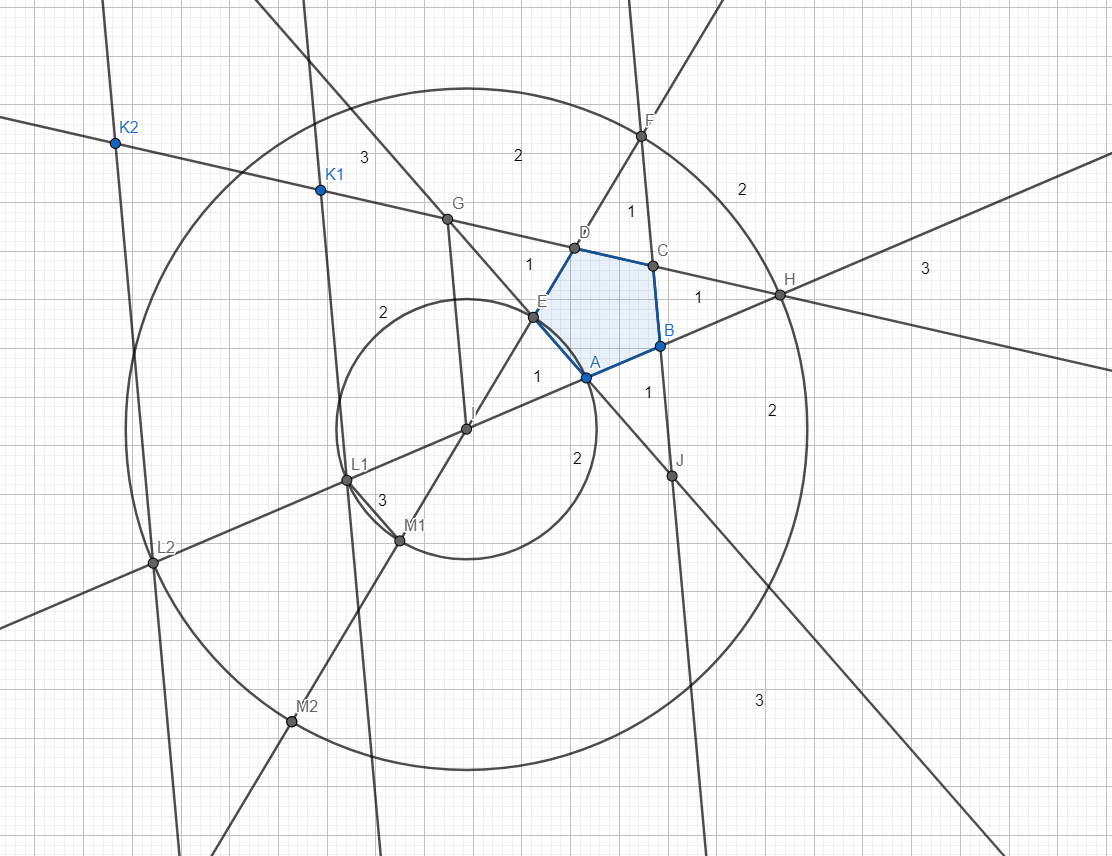
We shall keep the notations we used during the last solution. Since all the 2-areas and 3-areas are the same, we shall only look at one pair of such areas: The 3-area denoted by ED and AB, and the 2 area denoted by DC and AB. On the line DC, let us take the point $K_1$. Let \(L_1\) be the intersection of the line parallel to GI drawn through \(K_1\), and let \(M_1\) be a point on ED such that \(IL_1=IM_1\). Obviously, \(GIL_{1}K_{1}\) is an isosceles trapezium. Let \(x=GK_1\). The area of the trapezium \(GIL_{1}K_{1}\) is
\(A_{1}(x)=((GI+K_{1}L{1})/2)*h_{1}(x)\).
Since ABCDE is a regular pentagon, its angles are all equal to 108 degrees. After doing some angle chasing, we can deduce that the angles in \(GIL_{1}K_{1}\) are 108 degrees and 72 degrees.
$$K_{1}L_{1}=GI+2x*cos(18)$$
Thus,
$$A_{1}(x)=((2GI+2x*sin(18))/2)*(x cos(18))$$
$$=GI*xcos(18)+x^{2}*(sin(36)/2)$$
, and the area of \(IL_{1}M_{1}\), which is \(A_{2}(x)\), is equal to
$$A_{2}(x)=(x^{2}*sin(36))/2$$
Thus, $$[A_{1}(x))/(A_{2}(x)] = [GI*xcos(18)+x^{2}*(sin(36)/2)]/[x^{2}*(sin(36)/2)]$$. It is easy to observe that
$$\lim_{x\rightarrow infinity}\ (A_{1}(x)/A_{2}(x))=1$$, and, thus, the probability that the observer sees 3 sides is the limit towards infinity of \((A_{1})/(A_{1}+A_{2}+C)\), where C is the constant sum of the 1-areas and the small triangles in the 2-areas that weren't part of \(A_{2}(x)\).
This problem was really interesting to solve, and I pretty much enjoyed the fact that it could be solved through calculus. I am a geometry enthusiast, and combining geometry with ANYTHING else is amazing.
Ion Barbu, one of the great Romanian intellectuals (he was both a Mathematician and a Poet), once said that, and I quote, 'as contradictory as these subjects might be at first sight, there is, somewhere, in the higher planes of geometry, a place where it meets poetry.' I tend to agree with him, to be honest. I believe that the higher planes of geometry (I love this expression, it's kind of pun-y) intersect with many other fields of study, which I am eager to explore.
Cris.
'A man arrives at a random spot several miles from the Pentagon. He looks at the building through binoculars. What is the probability that he will see three of its sides?'
The fact that he watches through binoculars implies that we don't have to deal with the limitation of eyesight; we can presume, for the sake of this problem, that the man can see the Pentagon from a point infinitely far from the Pentagon.
I will present two solutions, one trivial (the solution proposed in the book; sadly, I didn't think of it), and my solution, involving calculus.

First solution:
Let us drawn the Pentagon and call it ABCDE. By intersecting the sides of the Pentagon, we can denote the areas in which the observer can see 1, 2 or 3 sides.
The drawing above shows the areas for which the observer sees 1, 2 and, respectively, 3 faces of the pentagon. Let us observe that, if the observer stays in a 2-area, then the symmetric of the observer through the center of the Pentagon, then the symmetric of the observer has an infinitely small chance of lying in the 1-area and a probability of being in a 3-area. Thus, the probability of the observer seeing 3 sides is the same as the probability of the observer seeing 2 sides, and the probability that the observer sees 1 side tends towards 0. Thus, \(P(1)+P(2)+P(3)=2P(3)=1\), so \(P(3)=1/2\).
Sadly, as I said, I couldn't see this solution when I solved the problem. Let me show you my solution.
Second solution:

We shall keep the notations we used during the last solution. Since all the 2-areas and 3-areas are the same, we shall only look at one pair of such areas: The 3-area denoted by ED and AB, and the 2 area denoted by DC and AB. On the line DC, let us take the point $K_1$. Let \(L_1\) be the intersection of the line parallel to GI drawn through \(K_1\), and let \(M_1\) be a point on ED such that \(IL_1=IM_1\). Obviously, \(GIL_{1}K_{1}\) is an isosceles trapezium. Let \(x=GK_1\). The area of the trapezium \(GIL_{1}K_{1}\) is
\(A_{1}(x)=((GI+K_{1}L{1})/2)*h_{1}(x)\).
Since ABCDE is a regular pentagon, its angles are all equal to 108 degrees. After doing some angle chasing, we can deduce that the angles in \(GIL_{1}K_{1}\) are 108 degrees and 72 degrees.
$$K_{1}L_{1}=GI+2x*cos(18)$$
Thus,
$$A_{1}(x)=((2GI+2x*sin(18))/2)*(x cos(18))$$
$$=GI*xcos(18)+x^{2}*(sin(36)/2)$$
, and the area of \(IL_{1}M_{1}\), which is \(A_{2}(x)\), is equal to
$$A_{2}(x)=(x^{2}*sin(36))/2$$
Thus, $$[A_{1}(x))/(A_{2}(x)] = [GI*xcos(18)+x^{2}*(sin(36)/2)]/[x^{2}*(sin(36)/2)]$$. It is easy to observe that
$$\lim_{x\rightarrow infinity}\ (A_{1}(x)/A_{2}(x))=1$$, and, thus, the probability that the observer sees 3 sides is the limit towards infinity of \((A_{1})/(A_{1}+A_{2}+C)\), where C is the constant sum of the 1-areas and the small triangles in the 2-areas that weren't part of \(A_{2}(x)\).
This problem was really interesting to solve, and I pretty much enjoyed the fact that it could be solved through calculus. I am a geometry enthusiast, and combining geometry with ANYTHING else is amazing.
Ion Barbu, one of the great Romanian intellectuals (he was both a Mathematician and a Poet), once said that, and I quote, 'as contradictory as these subjects might be at first sight, there is, somewhere, in the higher planes of geometry, a place where it meets poetry.' I tend to agree with him, to be honest. I believe that the higher planes of geometry (I love this expression, it's kind of pun-y) intersect with many other fields of study, which I am eager to explore.
Cris.
Inequality involving Lagrange Multipliers
I'm not a big fan of inequalities, as I can't really solve one without having a book with theory in front of me. Who knows, maybe I'll make a post about interesting inequalities once.
Even though I'm not really a big fan of inequalities, I am a fan of analysis, and this was my introduction to multivariable calculus, so I enjoyed this problem. Of course, my approach may not be the simplest; when I asked one of my friends over at a beer about this problem, he said that he could have solved it using elementary inequalities. If you can find a solution using only elementary inequalities, I encourage you to write it down below. The problem was taken, yet again, from an AoPS post.
The problem goes something like this:
If
First off, we have to find an interval in which lie all the solutions of the given equations.
Thus, by using CBS,
$$(x+y+z+t)^{2}<4(x^2+y^2+z^2+t^2) $$, which implies that $$(-u)^2<4(20-u^2)$$.
\(u^2<80-4u^2,\) so \(5u^2<80\), and, thus, \(-4<u<4\). Obviously, all the other variables satisfy the same condition. Now we know that x,y,z,t,u are in [-4,4]. Let us now denote the following functions defined on \([-4,4]^5\) with values in the reals:
$$g_1(x,y,z,t,u) = x+y+z+t+u$$
$$g_2(x,y,z,t,u)=x^2+y^2+z^2+t^2+u^2-20$$
$$f(x,y,z,t,u)=x^4+y^4+z^4+t^4+u^4$$.
We need to find the maximum value of the function $$F=f+ a g_1+ b g_2$$. Since \(f, g_1, g_2\) are derivable with a continuous derivative, the function F has a maximum on the given intervals, and, to find the maximum, we must differentiate F in x, y, z, t and u. In order to find the maximum, we must also use the fact that \(g_1=g_2=0\), which we know from the hypothesis.
After differentiating, we get the following set of equations:
$$4x^3+a+2xb=0$$
$$4y^3+a+2yb=0$$
$$4z^3+a+2zb=0$$
$$4t^3+a+2tb=0$$
$$4u^3+a+2ub=0$$
Since the equation $$4x^3+2xb+c=0$$ has a maximum number of three solutions, we can discern between two cases: One in which there are two pairs of equal numbers among (x,y,z,t,u), and one in which there are 3 equal numbers.
FIRST CASE: x=y, z=t.
We now have that \(2x+2y+u=0\) and \(2x^2+2y^2+u^2=20\). By writing \(u=-2(x+y)\), we get that
\(2x^2+2y^2+4(x+y)^2=20\), and, thus, \(6x^2+8xy+6y^2=20\), so \(3x^2+4xy+3y^2=10\) (1).
By rising to the second power, we get that \((3x^2+4xy+3y^2)^2=100\), and, thus,
$$9x^4+24x^{3}y+34x^{2}y^{2}+24xy^{3}+9y^4=100$$, and, multiplying it by 2, we get that
$$18x^4+48x^{3}y+68x^{2}y^{2}+48xy^{3}+18y^4=200$$
Now, \(x^4+y^4+z^4+t^4+u^4=2x^4+2y^4+16(x^4+4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^4 =\)
\(=18x^4+18y^4+64x^{3}y+64xy^{3}+96x^{2}y^{2}=\)
\(=200+16x^{3}y+16xy^{3}+28x^{2}y^{2}\),
which is smaller or equal to 260 if and only if
$$16x^{3}y+16xy^{3}+28x^{2}y^{2}<60$$and, by dividing by 2,
$$8x^{3}y+8xy^{3}+14x^{2}y^{2}<30$$which can be written as
$$xy(8x^2+8y^2+14xy)<30$$ (*)
We know that \(|u|=|-2(x+y)|<4\), so \(|x+y|<2\). By squaring, we get that \((x+y)^2<4\), and \(x^2+y^2>2xy, so xy<1\) (2).
Since \((x+y)^2=x^2+y^2+2xy<4\),
\(2x^2+4xy+2y^2<8\), while \(3x^2+4xy+3y^2=10\) (from (1)). Thus, we get a new inequality:
\(x^2+y^2>2\) (3)
Now, we write $$14xy=(28xy)/2=[70-21(x^2+y^2)]/2$$. Back to (*), we get that
$$xy(8x^2+8y^2+14xy)<xy[8x^2+8y^2+35-(21/2)(x^2+y^2)]=$$
$$(xy/2)[70+16(x^2+y^2)-21(x^2+y^2)]= (xy/2)[(70-5(x^2+y^2)]$$, which is, according to (3), smaller than $$(xy/2)(70-10)<30xy<30$$, so (*) is proven.
If you have come this far, I suppose you are curious about the second case, too. Writing this is kind of tedious, but fun nonetheless.
SECOND CASE: x=y=z
\(3x+u+t=0\), \(3x^2+u^2+t^2=20\), so \(u+t=-3x\) and \(u^2+t^2+2ut=9x^2\).
We also know that \(u^2+t^2=20-3x^2\), so \(ut=6x^2-10\)
Thus, \(t^4+u^4=(t^2+u^2)^2-2(tu)^2=\)
\(=400-120x^2+9x^4-2(36x^4-120x^2+100)=200+120x^2-63x^4\).
$$x^4+y^4+z^4+t^4+u^4=-60x^4+120x^2+200$$.
We have to find the maximum value of this expression on the interval [-4,4]. Let us write \(A=x^2\). Now, the function we have to evaluate is \(g(A)=-60A^2+120A+200\), which obviously has a maximum value, because it's a grade two function and the coefficient of the greatest power is negative.
By differentiating, we have to find the A for which $$g'(A)=-120A+120=0$$ only when \(A=1\), and, thus, the maximum value of \(x^4+y^4+z^4+t^4+u^4=260\).
Thus, after solving both cases, we can conclude that \(x^4+y^4+z^4+t^4+u^4<260\).
Note that, wherever I wrote <, I meant smaller or equal to something. I am still working on my Latex skills, and, for me, writing the full proof of this inequality was a feat of strength.
I have found another inequality that seems solvable with Lagrange Multipliers a while ago, yet I haven't solved it yet. If I manage to solve it, I'll make sure to post it. If you people have a solution to this problem that doesn't involve Lagrange Multipliers, please write it in the comments. I'm really curious about it :)
Cris.
Problem from an old Gazeta Matematica
'Gazeta Matematica' is the most well known mathematical journal in Romania, and it has been published continuously ever since 1895. The current owner of the journal is the Romanian Mathematical Society.
I have come across a rather interesting problem on AoPS recently, a problem concerning linear algebra. Here it is:
Let N be an odd number and A and B real N x N matrices such that the equation
\(det(A+xB)=det(B+xA)\)
has only integer roots. Prove that
\(|det(A-B)|=2^{\frac {n-1}{2}}\sqrt {det(A^2-AB)+det(B^2-AB)}\)
This problem first appeared in a number of Gazeta Matematica (we'll call it 'GM' for short) from 1991.
Here's the solution I offered on AoPS:
Consider the polynomial
\(P(x,y)=det(xA+yB)=det(A)x^n+a_1x^{n-1}y+...+a_{n-1}xy^{n-1}+det(B)y^n\)
Now, if we consider the polynomial
\(F(X)=det(A+XB)-det(XA+B)\)
.
Obviously,
\(det(A+XB)=P(1,X), det(XA+B)=P(X,1)\).
By substituting the two determinants, we find out that
\(F(X)=(detA-detB)+x(a_1-a_{n-1})+...+x^n(detB-detA)\) .
Its roots have product equal to 1, from Viete's formulas. Thus, since all the roots are in
\(F(X)=(detB-detA)(X-1)^n\)
.
By writing
\((detB-detA)(X-1)^n=det(A+XB)-det(XA+B)\).
,
and replacing x with -1, we get a nicer form of the conclusion.
I found this problem to be a nice linear algebra exercise, as it tested the student's ability to juggle between polynomials and matrices. It wasn't really hard, but it was interesting nonetheless.
NOTE: I have included the Maths as photos. This process takes a long while, I really hope I figure out a better way of writing the Maths as soon as possible.
Cris.
Welcome!
Welcome, people, to my first blog! I will try to write about a great deal of interesting things here, all scientific (more or less) in nature.
However, the aim of this blog is to promote Mathematics. Most of the articles I'll post will be closely related to Mathematics, and I will also post problems that I found intriguing. I will accompany each problem with a solution and the author's name or the place from where I took it, if the author's name is unavailable.
I've got to thank my friend Alex, who helped me with the layout of the website. He will also post interesting articles regarding computer science from time to time, so he is one of the authors. He came up with the idea of making a whole section regarding theory in Maths and Computer Science, which we'll upload soon.
Without further ado, let's get right into it! Hope you have a great time on my blog, and I hope you will enjoy the articles I'll post just as much as I'll enjoy writing them.
Cris.
Subscribe to:
Posts (Atom)
