Two Linear Algebra problems of completely different flavours

Eyy, what's up - what's down? I have my final high school exams this week, and, after that, I'll be free to study anything I want. I already started looking into tensor products and metric spaces (I know, kinda unrelated), and I really hope I can upgrade the level of Maths on this blog by the end of summer. I really wish to learn more advanced Maths topics, so I could also do some neat Physics.

Anyways, before my final exams, I thought that I should post something fun, in case I don't make it lmao. So here are my picks for this article! Of course, they are linear algebra problems, but I promise I will soon change the topic. As much as I'd love linear algebra (it's my favourite part of Mathematics at the moment), this blog is called 'Cris's Science Blog', not 'Cris's Linear Algebra Blog'.

The first problem comes from an Excellence Test from Timisoara. I was searching through some old Mathematical magazines of mine, and I found a remarkable number from the RMT (Revista Matematica Timisoara, the Mathematical Magazine of Timisoara), the one made for the 2017 Maths Olympiad. Of course, it brought back memories, since that was my brightest year. That particular number was dedicated to the memory of one of the greatest Mathematics teachers Romania ever had, Gheorghe Eckstein.

This problem looks like an X and O with matrices. Suppose you have a \(2n * 2n\) matrix, that is 'empty' at first. Two players, A and B, take successive  turns at writing numbers in the matrix. Once a number was written, it can't be erased. A wins if the determinant of the matrix isn't 0, while B wins if the determinant is 0. The question asks if there exists a strategy for which B always wins, no matter what A does.

Solution: After playing with my imaginary friends for a while, I figured out that there is, indeed, a strategy. Since the matrix doesn't involve any known numbers, it was safe to assume that the strategy consisted of doing something with the lines of the matrix.

Consider the first two lines of the matrix. If A puts a number \(x\) on the first line, B should put the same number right under it. By repeating this process, there will be two equal lines. Since the number \(2n\) is even, B will always be the one ending the process, and, thus, he will be in control of the determinant. It doesn't matter what A puts in the other lines; if A puts a number on one of the other lines, B can randomly put a number there, too. Eventually, A will be the one writing a number on one of the first lines, and B will duplicate that number.

The problem wasn't exactly hard, but it was a fun game. That's why I added the 'Intriguing Puzzles' tag.

Now comes a more scientific one. This one is taken from Evan Chen's 'Napkin'. I started studying University Maths from there, and I really recommend checking it out: http://web.evanchen.cc/napkin.html

Let V be a finite dimensional vector space, and let \(T: V->V\) be a linear map, and let \(T^n:V->V\) denote T applied n times. Prove that there exists an integer N such that \(V=Ker(T^N)⊕Im(T^N)\).

Solution: In order to talk about a direct sum, I want to prove that there is an N after which \(Ker(T^N)⋂Im(T^N)=Φ\). It is easy to see that, as N increases, the Kernel of the linear map increases, while the dimension decreases. Since V is finite dimensional, the dimension of the Kernel reaches a maximum, let's call it l. I want to prove that, after it reaches this maximum, the Kernel and the Image become distinct. Since the dimension of the Kernel remains the same, it is obvious that the Kernel will remain the same after iterations. Let N be the iteration of T for which the Kernel remains constant afterwards.

Let \(a\) be in both \(Ker(T^{N+1})\) and \(Im(T^{N+1})\). I want to prove that \(a=0\). We know that \(T^N(a)=O\), and, since a is in the image, we have that \(T^{2N+1}(b)=0\), for b, the pre-image of a. Thus, we know that b is in \(Ker(T^{2N+1})=Ker(T^{N})\). But, since \(T^{N+1}(b)=a\), we get that \(a=0\), exactly as we wanted, so we can talk about a direct sum.

Now, we know that \(dim (Ker(T^N) ⊕ Im(T^N)) = dim Ker(T^N) + dim Im(T^N) = dim V\), and, since the Kernel and the image are subspaces of V, we get that their direct sum is exactly V, as we wanted.

I found this problem rather interesting, and, from what I saw, it works as a lemma. I haven't tried writing this as actual vector spaces instead of abstract notations, but I might look into it. Until then, I have to study Literature for my exam on Monday. Wish me luck, and more posts are coming! At first, they'll still be Linear Algebra, but after a while, trust me, they'll become more diverse. Tune in next time for something completely random about matrices!

Cris.

Invariant of 4 congruent triangles

I'm back to the usual content, everyone! Well, not really usual, since this problem is more of a puzzle than a problem, but you get the point. No more psychology articles for a while. Anyways, this puzzle comes from the Moscow Maths Olympiad (or the Mexican Maths Olympiad; I don't really know what MMO stands for when it comes to Maths) from 1995, and it goes something like this:

Suppose you have 4 congruent right-angled triangles. After each step, we cut one of the triangles along its height. Prove that, after any number of steps, there are still at least 2 congruent triangles.

Solution:

Let the division of the longer leg of the triangle over the smaller leg be equal to \(x\). Thus, when we cut a triangle along the height, we get two smaller triangles with areas proportional to \(x\) and \(1-x\). Let us presume that the initial area of the triangles is 1. At the first step, we have 4 triangles, which have \(x\) and \(1-x\) 0 times in the formula of their areas, so we write that 

$$S(0) = (0,0) (0,0) (0,0) (0,0).$$

After the first step, one triangle is split in two parts, one of area \(x\) and one of area \(1-x\), so 

$$S(1) = (1,0) (0,1) (0,0) (0,0) (0,0)$$ because \(x\) and \(1-x\) appear only once in the formula of the area of two triangles. Continuing this, we get that, at the p-th step, 

$$S(p) = (m_1, n_1) (m_2, n_2) ... (m_{p+4}, n_{p+4})$$ 

You may see where I'm going with this. We can represent all these pairs as positive lattice points. For two triangles to be congruent, their respective lattice points must be the same. Now, let us presume that, at the start of the game, we put 4 coins of value 1 on the lattice point (0,0). After the first step, we move half a coin on (1,0) and half a coin on (0,1), and, after each step, this process continues. In order for two triangles to be congruent, there must be 2 coins on at least one lattice point. We shall prove that, if there is one coin in all the lattice points, then the sum of values is smaller than 4, which should conclude the proof. 

The number of coins on each lattice point is dependent on the position of the lattice point. The coins in the point (m,n) have value \(2^{-m-n}\). Thus, we have to prove that 

$$\sum_{n∈ℕ} \frac {n+1}{2^n}<4$$

This series, as shown by Wolfram Alpha (https://www.wolframalpha.com/input/?i=sum+n%3D0...+infinity+(n%2B1)%2F2%5En), converges to 4, and is strictly increasing, so the value of the coins is always smaller than 4, which leads to a contradiction. The series could have been proven to be smaller than 4 by hand, but I preferred using Wolfram Alpha for a quicker result. 

Since the sum of values in all positive lattice points is 4, this means that at least a lattice point has 2 coins on it, which concludes the proof.

I found this problem really interesting, mainly because of the ingenuity required to solve it. I found it in Arthur Engel's excellent book 'Problem Solving Strategies' (did you really think I'd go as far as to search the Mexican Maths Olympiad from 1995?) while preparing for my interview at Oxford. Apologies for not posting anything for the past two weeks, I was in Oxford for about a week, and then I had to catch up with my homework, so it has been a pretty rough period. Tune in next time for the first post under the 'Theory' tag, which has been a long time coming! 

Cris.

Ant on a Cube

First of all, apologies for not posting much lately. I've been really busy preparing for Olympiads/admission exams. I will probably post a lot more after the admission process is over (probably in December), but, until then, I might be a little bit inactive. As placeholders, I shall post some interesting puzzles. Here's one of them, which I took from the 2001 Oxford MAT.

A set of 12 rods, each 1 metre long, is arranged so that the rods form the edges of a cube. Two corners, A and B, are picked with AB the diagonal of a face of the cube. An ant starts at A and walks along the rods from one corner to the next, never changing direction while on any rod. The ant’s goal is to reach corner B. A path is any route taken by the ant in travelling from A to B.

(a) What is the length of the shortest path, and how many such shortest paths are there?
(b) What are the possible lengths of paths, starting at A and finishing at B, for which the ant does not visit any vertex more than once (including A and B)?
(c) How many different possible paths of greatest length are there in (b)?
(d) Can the ant travel from A to B by passing through every vertex exactly twice before arriving at B without revisting A? Give brief reasons for your answer.

Solution:

Consider the following cube in the 3D space.


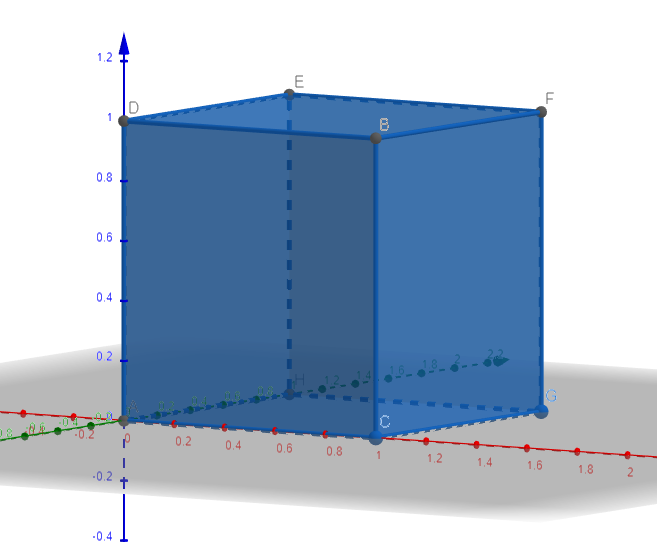
The coordinates of the edges are A(0,0,0), B(1,1,0), C(1,0,0), D(0,1,0), E(0,1,1), F(1,1,1), G(1,0,1).
Let's make some quick observations. First of all, in order to get from (0,0,0) to (1,1,0), one must make an even number of steps on the \(O_z\) and an odd number of steps on \(O_x\) and \(O_y\), where a 'step' means going from one vertex to another one via the rod linking the vertexes. Thus, the total number of steps is even. The number of steps minus 1 is the number of vertexes the ant passes through. Thus, any route leading to B (a route is a collection of steps) involves an odd number of vertexes.

a) The two shortest paths are obviously A-C-B and A-D-B, each having length 2.

b) Since the ant doesn't visit each vertex more than once and the number of vertexes is 8, then it means that the maximum number of vertexes in a route is 7, because the number of vertexes must be odd. We know that the number of steps on \(O_z\) is even, so we have three cases: if the number of steps on \(O_z\) is 0, if the number of steps on \(O_z\) is 2 and if the number of steps on \(O_z\) is 4. However, there is no route with 4 steps on the \(O_z\) axis. If there was such a route, then all the 8 vertexes would be involved, because the ant can only visit each vertex once. Thus, the number of vertexes in the route would be bigger than 7, contradiction.
If the number of steps on the \(O_z\) axis is 0, then we have the routes described in a)
If the number of steps on the \(O_z\) axis is 2, then we can find the route A-H-E-D-B to be possible. This route has length 4, so 4 is a possible length. We can find the route A-H-E-F-G-C-B of length 6, too, so 6 is also a possible length. The route A-H-E-F-G-C-B passes through 7 vertexes, so 6 is the maximum length of a route.
Thus, the possible lengths are 2, 4 and 6.

c) There are 8 paths of length 6: \(A-H-E-F-G-C-B\), \(A-H-G-F-E-D-B\), \(A-C-G-F-E-D-B\), \(A-C-H-H-E-D-B\), \(A-C-G-H-E-F-B\), \(A-D-E-F-G-C-B\), \(A-D-E-H-G-F-B\), \(A-D-E-H-G-C-B\).

d) If the ant travels through each vertex other than A and B twice, then it means that it passes through 14 vertexes, which contradicts the fact that a route from A to B passes through an odd number of vertexes. Thus, such a journey is impossible.

The solution offered by the people making the MAT was similar to what I did. While solving this problem, I remembered of a problem from Thomas Povey's excellent 'Professor Povey's Perplexing Problems', which regarded the number of ways in which an ant can get from an edge of the cube to the opposing edge in a certain number of ways. I was a bit surprised to see a problem using 3D geometry in the MAT, but then I remembered that the A-level core curriculum was a lot more different in 2001 than it is now. Before that, things were even more awkward. I even encountered introductory elements of group theory in a STEP 1 from the 80's. Those times were a lot more...interesting...

Cris.

The Probability of Passing a Test

Have you ever attended a test without studying anything whatsoever before it? Well your boy Cris is here to tell you something: you most certainly failed. Or, at least, you would have most certainly failed in a world fully governed by A-level Mathematics. I managed to find last year's STEP today, and I decided to take a look at some of the problems. Apart from the tedious, VERY TEDIOUS calculations, I found a nice problem that many people will emphasize with. This problem was the last Probability exercise in Step 1 last year.

A multiple-choice test consists of five questions. For each question, n answers are given
(n > 2) only one of which is correct and candidates either attempt the question by choosing
one of the n given answers or do not attempt it.
For each question attempted, candidates receive two marks for the correct answer and lose
one mark for an incorrect answer. No marks are gained or lost for questions that are not
attempted. The pass mark is five.
Candidates A, B and C don’t understand any of the questions so, for any question which
they attempt, they each choose one of the n given answers at random, independently of their
choices for any other question.
(i) Candidate A chooses in advance to attempt exactly k of the five questions, where
k = 0, 1, 2, 3, 4 or 5. Show that, in order to have the greatest probability of passing
the test, she should choose k = 4 .
(ii) Candidate B chooses at random the number of questions he will attempt, the six
possibilities being equally likely. Given that Candidate B passed the test find, in
terms of n, the probability that he attempted exactly four questions.
(iii) For each of the five questions Candidate C decides whether to attempt the question
by tossing a biased coin. The coin has a probability of \(\frac{n}{n+1}\) of showing a head, and
she attempts the question if it shows a head. Find the probability, in terms of n, that
Candidate C passes the test.

Solution:
(i) The probability of getting a correct answer to a question is \(\frac{1}{n}\). If k is smaller than 3, then the passing score isn't achieved in any scenario, so the probability of passing for k<3 is 0.
If k=3, then the probability is \(\frac{1}{n^3}\).
If k=4, then the probability of passing is \({4}\choose{3}\)\(\frac{n-1}{n^4}+\frac{1}{n^4}=\frac{4n-3}{n^4}\).
If k=5, then the probability of passing is \( {5}\choose{4}\)\(\frac{n-1}{n^5}+\frac{1}{n^5}\). In the last case, the minimum number of possible correct answers is 4, because otherwise the passing mark isn't achieved. Let us now compare the probabilities we found.
$$\frac{4n-3}{n^4}>\frac{1}{n^3}⟺4n-3>n⟺n>1$$.
$$\frac{4n-3}{n^4}>\frac{5n-4}{n^4}⟺4n^2-3n>5n-4⟺4(n-1)^2>0$$
Thus, the biggest probability of passing is when k=4.

(ii) We shall use Bayes' theorem for this one. Bayes' theorem states that, if we want to calculate the probability that the even B happens given that another event A happened before, then the probability required is \(P(B|A)=\frac{P(B⋂A)}{P(A)}\). Thus, the probability of B passing is $$P(k=4|pass)=\frac{P((k=4)⋂pass)}{P(pass)}=$$
$$=\frac {\frac{4n-3}{n^4}}{\frac{5n^2+2n-4}{n^5}}=$$
$$=\frac{4n^2-3n}{5n^2+2n-4}$$

(iii) \(P(C|pass)=\frac{10n^3}{(n+1)^5}*\frac{1}{n^3}+\frac{5n^4}{(n+1)^5}*\frac{4n-3}{n^4}+\frac{n^5*(5n-4)}{n^{5}*(n+1)^{5}}=\frac{25n-9}{(n+1)^5}\).

The problem itself was rather easy, and the calculations were simple enough to be done quick enough. The Step this year had some really interesting geometry problems, and, from what I've heard, had a monster algebra problem. While I find Step questions insanely interesting, I find the calculations required a bit tedious.

I attended a contest similar to the one described in the problem when I was younger. I am pretty sure many kids across the world, too, participated at the Mathematical Kangaroo competition. It was a rather good mental exercise for kids, in which you were asked to solve 30 questions in an hour and a half or something. I never did good in multiple choice tests, so I didn't have insanely good results at it; if I recall correctly, I once started crying desperately in one such contest, and the teacher assisting us was afraid to take my paper when the time concluded. Yikes!

Cris.

Making a tour of a square grid

The new design update of the blog deserves a content update too, don't you think? This problem is part of the 'Intriguing Puzzles' series, which I will post from time to time.

This specific puzzle is rather well known, and I am sure that most people may recognize this. There are lots of puzzles regarding 'tours' of certain buildings; by tour, I mean going through each room only once and then returning to the starting room. There is a problem, however: not all buildings can be toured. For this puzzle, we will consider a nxn rectangular grid. Let us look at a 5x5 grid.

We shall prove that such rectangular grids can't be toured. I came across this problem in the Oxford Mathematics Aptitude Test from 2009, yet I am sure that it was posed many times before.

By absurd, we shall presume that the grid can be toured.

Let us color the rectangular grid in black and white like a chessboard:



A 'move' is defined as the movement from one room to a neighboring room. Let us observe that, if a tour starts in a room of a certain color, it takes an even number of moves to return to a room of the same color. A tour of a grid should consist as \(n^2\) moves, as that's the number of rooms you need to tour. In the case of an odd n, the number of rooms is odd, so the number of moves is odd. Thus, after \(n^2\) moves, you can't return to a room of the same color as that of the room you started from, resulting in a contradiction.

The problem given by Oxford was more complicated than this; this was the last part of the problem given at Oxford. In the first four parts, you had to deal with a rectangular \(n*n\) grid with an even n. This problem reminds me of a puzzle regarding covering a chessboard with dominoes because of the strategy used. But that's a puzzle for another time.

Cris.