Invariant of 4 congruent triangles

I'm back to the usual content, everyone! Well, not really usual, since this problem is more of a puzzle than a problem, but you get the point. No more psychology articles for a while. Anyways, this puzzle comes from the Moscow Maths Olympiad (or the Mexican Maths Olympiad; I don't really know what MMO stands for when it comes to Maths) from 1995, and it goes something like this:

Suppose you have 4 congruent right-angled triangles. After each step, we cut one of the triangles along its height. Prove that, after any number of steps, there are still at least 2 congruent triangles.

Solution:

Let the division of the longer leg of the triangle over the smaller leg be equal to \(x\). Thus, when we cut a triangle along the height, we get two smaller triangles with areas proportional to \(x\) and \(1-x\). Let us presume that the initial area of the triangles is 1. At the first step, we have 4 triangles, which have \(x\) and \(1-x\) 0 times in the formula of their areas, so we write that 

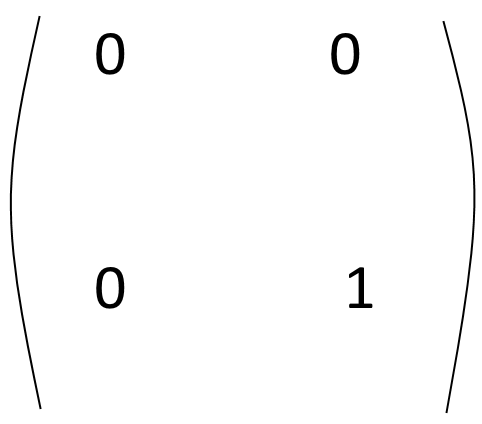
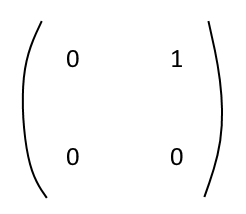
$$S(0) = (0,0) (0,0) (0,0) (0,0).$$

After the first step, one triangle is split in two parts, one of area \(x\) and one of area \(1-x\), so 

$$S(1) = (1,0) (0,1) (0,0) (0,0) (0,0)$$ because \(x\) and \(1-x\) appear only once in the formula of the area of two triangles. Continuing this, we get that, at the p-th step, 

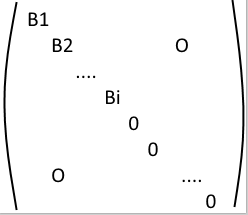
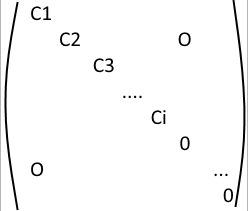
$$S(p) = (m_1, n_1) (m_2, n_2) ... (m_{p+4}, n_{p+4})$$ 

You may see where I'm going with this. We can represent all these pairs as positive lattice points. For two triangles to be congruent, their respective lattice points must be the same. Now, let us presume that, at the start of the game, we put 4 coins of value 1 on the lattice point (0,0). After the first step, we move half a coin on (1,0) and half a coin on (0,1), and, after each step, this process continues. In order for two triangles to be congruent, there must be 2 coins on at least one lattice point. We shall prove that, if there is one coin in all the lattice points, then the sum of values is smaller than 4, which should conclude the proof. 

The number of coins on each lattice point is dependent on the position of the lattice point. The coins in the point (m,n) have value \(2^{-m-n}\). Thus, we have to prove that 

$$\sum_{n∈ℕ} \frac {n+1}{2^n}<4$$

This series, as shown by Wolfram Alpha (https://www.wolframalpha.com/input/?i=sum+n%3D0...+infinity+(n%2B1)%2F2%5En), converges to 4, and is strictly increasing, so the value of the coins is always smaller than 4, which leads to a contradiction. The series could have been proven to be smaller than 4 by hand, but I preferred using Wolfram Alpha for a quicker result. 

Since the sum of values in all positive lattice points is 4, this means that at least a lattice point has 2 coins on it, which concludes the proof.

I found this problem really interesting, mainly because of the ingenuity required to solve it. I found it in Arthur Engel's excellent book 'Problem Solving Strategies' (did you really think I'd go as far as to search the Mexican Maths Olympiad from 1995?) while preparing for my interview at Oxford. Apologies for not posting anything for the past two weeks, I was in Oxford for about a week, and then I had to catch up with my homework, so it has been a pretty rough period. Tune in next time for the first post under the 'Theory' tag, which has been a long time coming! 

Cris.

A Cheerful Introduction to Jungian Functions

I haven't released an article in about a week... oh boy. I've been advertising this article for a while now, so I'll do all my best to make it count. Next article might be about an inequality, but, until then, the number of Maths posts on this blog remains the same.

In this article, I will introduce you (if you weren't already introduced) to Jungian Psychology and its successor, the Myers-Briggs Type Indicator, MBTI for short. Perhaps I will discuss Socionics in a sequel to this article (if there will be a sequel to this article). It isn't a pleasant thought to think that I am writing an article on personality types when I can't even decide what my type is...

Carl Jung, in his book 'Psychologial Types', discussed the problem of types in different contexts and observed several patterns. Other than historical contexts, Carl Jung observed these patterns in his work as a psychiatrist. Other than the classical 'Extrovert' vs 'Introvert' options, he also discovered something he called 'cognitive functions', which are basically ways of perceiving/judging the world. Each person has a personality formed by a permutation of the 8 possible cognitive functions, which I'll discuss shortly.

Each function is composed of two letters: the first letter is the preferred type of perceiving/judging, while the second letter explains how the user of the function uses it, whether he uses it in an introverted manner or an extroverted manner.

The perceiving functions do literally what the name says: they perceive information. A person can perceive information either by sensing or by intuition: the intuitive person will read between the lines, they process information through possibilities, hidden meanings and impressions, while the sensing person will perceive information through the body senses. The perceiving functions are:

• Ne: Extroverted intuition. This one is the impersonation of every mad scientist in movies. People with Ne as one of their first two functions are highly creative individuals. They are characterized by their need for debate and meaningful discussion, and also by their hatred for rigid environments. They are free-spirited individuals who enjoy life. 
• Ni: Introverted intuition. This one is the deepest of the cognitive functions, as it is intimately linked with the subconscious. Individuals with this cognitive function as one of their first two functions in the stack can use most of the brain in order to predict how events turn out, it basically works as a glimpse into the future, making these people look like prophets. People with this personality function are also the main antagonists in movies. Such humans have incredible mental landscapes, making Ni one of the most creative functions.
• Se: Extroverted Sensation. This one is the most adventure-seeking function. These people thrive on intense experiences, and people with this function as one of their first two functions in the stack are some of the most thrill-seeking people. This function basically lives in the present, and can notice details about recent events quite nicely.
• Si: Introverted Sensation. This one is the most calm of them all. People like this perceive new information through a prism of old experiences and sensations. This function is the most melancholic of them all, and also the most common one, as about 30-40% of the population has this function as either their primary or secondary function. This function is also correlated with good memory.

The judging functions, just like the perceiving ones, do literally what their name says. A person can judge given information through the lens of either feelings and values or logical reasoning. The judging functions are:

• Fe: Extroverted Feeling. This is widely considered as the most extroverted function, as it involves connecting on a personal level with most of the people a person knows. People with Fe among their first two cognitive functions are very popular and great talkers, they are empaths with a great desire to help people. However, people like this may be also manipulative, as they have an intuitive knowledge of what other people want. This function usually involves sync-ing in with other people's feelings and with the social norms, and it requires a great deal of socializing for it to flourish.
• Fi: Introverted Feeling. While the Fe function adheres to the social norms, this function draws values from within. People with Fi as the first are very idealistic and romantic, they are easily influenced by people, but they are mostly trying to do good.
• Te: Extroverted Thinking. This function is the one most concerned with efficiency. People with this function among their first 2 functions are obsessed by the efficiency of their actions, and all of their judgements are objective and impersonal.
• Ti: Introverted Thinking. This function is the one obsessed with problem solving (aka the part of me making this blog). It is derived from an internal logical system and thrives on solving problems from all possible subjects. 

These are, more or less, the cognitive functions. Each individual possesses, in some measure, all of the cognitive functions above. Jung believed that each individual has a primary and auxiliary function (hence why I talked about the first two functions), and these functions reflect the individual's attitude the most. In the next psychology article, I will discuss about the MBTI model of describing a personality, which is basically a consequence of the Jungian model. Keep in mind that, while there isn't much evidence to back up this theory, it resembles reality the most, which is why I decided to write about it. Another thing to mention is that no two individuals who have the same cognitive functions are the same. I've heard many arguments that categorizing people is wrong, which, in some cases, is true. However, in the case of psychological types, it's not wrong to categorize people, and it's a fairly logical thing to do. The cognitive functions don't describe WHAT a person thinks, but rather HOW a person thinks, which, in my opinion at least, makes the cognitive functions model almost foolproof to such arguments.

Cris.

Calculating the limit of a sum using the Riemann-Zeta function

Remember when I said that the next article would be the psychology article or an inequality article? Well...

I took the following problem off of Brilliant and I decided to make it a little bit tougher. I have to admit, the idea of using the Riemann-Zeta function didn't come to mind when solving the problem, but I decided to post it nonetheless, because it's rather interesting. As a reminder, the Riemann-Zeta function is defined as \(ζ(s)=\sum_{i=1}^{\infty} i^{-s}\). The Riemann Hypothesis, an open problem in Mathematics, is about a property of this function, namely that all 0-s of this function lie on the line \(Re(x)=\frac{1}{2}\). 

Back to the problem at hand: what is the value of $$\sum_{n∊ℕ}\frac{2^{w(n)}}{n^2}$$ where \(w(n)\) is the number of prime divisors of n.

Solution:

First off, even though an approximation of \(w(n)\) sounds plausible, believe me, it's not. We shall write this sum in a more comprehensible manner. Let us observe that, for a certain number n, the number of ways of writing n as a product of two coprime numbers is equal to \(2^{w(n)}\), so \(\sum_{n∊ℕ}\frac{2^{w(n)}}{n^2}=\sum_{(a,b)=1}\frac{1}{(ab)^2}\). Now, we know that \(\sum_{a,b∊ℕ}\frac{1}{(ab)^2}=(\sum_{a∊ℕ}\frac{1}{a^2})*(\sum_{b∊ℕ}\frac{1}{b^2})=ζ(2)^2\). In order to find this sum for coprime numbers, let us consider \(a=cm,b=cn\), with \(c\) a natural number and \((m,n)=1\). Thus, $$\sum_{a,b∊ℕ}\frac{1}{(ab)^2}=\sum_{m.n,c∊ℕ}\frac{1}{c^4 m^2 n^2}=$$ $$=(\sum_{c∊ℕ} \frac{1}{c^4})(\sum_{(m,n)=1} \frac{1}{(mn^2)})$$

Thus, the required sum is \(\frac{ζ(2)^2}{ζ(4)}=2.5\), which concludes the proof. Of course, there is a generalization to this problem for \(n^m\) rather than \(n^2\), which is solvable through the same method and yields the result \(\frac{ζ(n)^2}{ζ(2n)}\). This was the first time when I actually used the Riemann-Zeta function in a problem, and it gave me a satisfying feeling, even though, as I said, the proof isn't completely mine. Brilliant has a great stash of great problems like this, so you should check them out.

Apologies for the fact that I haven't posted in two weeks, but I am very stressed out due to this whole application process and, since this is my terminal year of high school, I must prepare for the exams at the end of the year. There's also the fact that I am still thinking about how to solve the inequality I wanted to write about, and the fact that writing anything non-mathematical in nature, such as the psychology article, is a bit tough and requires some background checks... so I suppose that you should expect something completely random in the next article. 

Cris.

Intersection of 3 Proper Subgroups

Welcome back to the world of magic Math tricks! Today we shall be covering an interesting problem that I found a few days ago on AoPS regarding the intersection of 3 proper subgroups (duh...). Apparently the problem was first proposed in the 9th number of 'Gazeta Matematica' from 1985. I surely do love problems that are older than me.

Let \(G\) be a group and \(H_1, H_2, H_3\) be proper subgroups of \(G\) such that \(G= H_1 \cup H_2 \cup H_3\)

Prove that \(x^2 \in H_1 \cap H_2 \cap H_3\) for all \(x \in G\).

Solution:

First of all, let us prove that none of this subgroups includes another. Let's presume by absurd that \(H_2\) is contained in \(H_1\). This would imply that \(H_1 \cup H_3 = G\), which, in turn, would imply that either \(H_1\) or \(H_3\) is \(G\), which contradicts the fact that the subgroups are proper. This argument works if one group is included in the reunion of the others, too.

If \(x \in H_1 \cap H_2 \cap H_3\), then it is obvious that \(x^2 \in H_1 \cap H_2 \cap H_3\).

If \(x \in H_1 \cap H_2 - H_3\), then we shall do a magic trick and write \(x^2=xaa^{-1}x\), where \(a \in H_3 - H_1 \cup H_2\). \(xa\) obviously doesn't belong to \(H_1 \cup H_2\), so it must be in \(H_3\). This argument works for \(a^{-1}x\), too, so \(x^2 \in H_1 \cap H_2 \cap H_3\). The other possible intersections of these groups can be treated the same.

If \(x \in H_1 - H_2 \cup H_3\), then we write \(x^2=xaa^{-1}x\) again, this time with \(a \in H_2 - H_1 \cup H_3\). Obviously, \(xa\) can't be in either \(H_2\) or \(H_1\), so it is in \(H_3\), so \(x^2 \in H_3\). By choosing a suitable \(b \in H_3 - H_1 \cup H_2\), we get that \(x^2 \in H_2\), so \(x^2 \in H_1 \cap H_2 \cap H_3\). All similar cases are treated as above.

This little exercise can work as a Mathematical 'Creativity Test' if you think about it, because it's about discerning a certain pattern and coming up with an idea that solves the problem instantly. More posts might be coming this week, as I am working on 2 more articles atm: the psychology article (finally) and another one with partial derivatives / Lagrange multipliers. Tune in next time for one of these articles (probably the psychology article will come first)!

Cris.

Isomorphic groups of integer matrices

My dudes, buckle up, because we're exploring the wonderful realm of abstract algebra again. I found the following problem in the latest number of the 'Gazeta Matematica' by a teacher called Dan Moldovan. I've got to say, the problem is amazing, and I thank this professor for proposing it.

Let \(m,n,p>2\) be natural numbers and let \(G=[A_1, A_2, ... A_p]\) matrices in \(M_{n}(Z)\). To every matrix in G, we attach the reduced matrix modulo m, \(\hat A_i\), so that, if \(A_i=(a_{i,j})\) is out matrix, then the reduced matrix is \(\hat A_i≡(\hat a_{i,j}\), where \(\hat a_{i,j}=a_{i,j}\)(modulo m). Prove that \(\hat G=[\hat A_1, \hat A_2,...\hat A_p]\), together with multiplication in \(M_n(Z)\), forms a group that's isomorphic with G.

Solution:

First of all, let us observe that the neutral element of G isn't \(I_n\). I know this sounds counter-intuitive, but take the group formed by an idempotent matrix with multiplication. The neutral element there is the matrix itself, so any idempotent matrix can be the neutral element of this group. For the sake of the problem, we shall consider the neutral element of G as \(I\). \(I\) has the property that \(I^2=I\), and \(AI=IA=A\) for any element \(A\) in G.

Let us consider the case in which \(I=O_n\). In this case, \(AO_n=A=O_n\), so G={\(O_n\)}, and \(\hat G=[\hat O_n]\), so the two groups are isomorphic.

If \(I\) is different from \(O_n\), then we shall prove that \(gcd(I)=1\). Let \(x=gcd(I)\), and it follows that \(I=xB\), where B is another matrix in \(M_n(Z)\). Since \(I^2=I\), \(x^2B^2=xB\), so \(xB^2=B\). Since \(B^2\) is different than 0 (because otherwise \(I=O_n\)), x divides all elements in B, so \(x^2\) divides all elements of I, which implies that \(x=1\).

I found the following lemma in the excellent article 'Finite Groups of Matrices Whose Entries Are Integers', published in AMC in 2002 by Mr. James Kuzmanovich and Mr. Andrey Pavlichenkov.(https://www.jstor.org/stable/2695329)

Lemma: Let G be a group of integer matrices in which there is an element \(A\) such that \(A^q=I\), with q prime, and \(\hat A=\hat I\), where \(\hat A\) is the reduced matrix modulo p, where p is another prime number. It follows that \(A=I\).

Proof: Since \(\hat A=\hat I\), \(A=I+pH_1\). Let \(gcd(H_1)=d\)
⟹\(A=I+pdH\), where \(gcd(H)=1\).
⟹\(A^q=(I+pdH)^q=I+\sum_{k=1}^q {{q}\choose{k}}(pd)^{k}H^k I^{q-k}=I\). However, \(I^n=I\), for all n, so \(\sum_{k=1}^q {{q}\choose {k}}(pd)^{k-1}H^k I=O_n\) (I divided by \(pd\). The only element without \(p\) in it is is \(qHI\), so p divides q, and, thus, p is q or p is 1. Since p is prime, p is q, and, by dividing the relation once more, we get that p divides \(gcdH\), so p is 1, which is a contradiction. Thus, \(H=O_n\), so \(A=I\).                           

Back to our problem, I shall prove something that probably everyone saw coming: the fact that \(f(X)=\hat X\) is the isomorphism we were looking for, where \(\hat A\) is the reduced matrix modulo m. Obviously, \(\hat I\) is the neutral element in \(\hat G\), and all the calculations are the same, so f is a morphism. Since \(G\) and \(\hat G\) are finite, we have to prove that the morphism is injective. For that, we shall prove that \(Ker (f)=[I]\).

Let us presume by absurd that there is an A in G such that \(f(A)=\hat A=\hat I\). Thus, \(A=I+mB\), so, because G has order p, \((I+mB)^p\). Let q be a prime factor of p. Thus, we have that
$$⟹((I+mB)^\frac{p}{q})^q=I$$
Since \(\frac {p}{q}=k\) is an integer, \((I+mB)^k=I+mH_1\), so \((I+mH_1)^q=I\).
$$⟹\sum_{j=1}^q {{q}\choose{k}}(mH_1)^j I=O_n$$
Let \(gcd H_1=d\), so \(H_1=dH\), with \(gcd(H)=1\). Thus,
$$\sum_{j=1}^q (md)^{j-1}H^j I= \sum_{j=1}^q (md)^{j-1} H^j =O_n$$
By using the same logic as before, \(md | qH\). Since \(gcd(H)=1\), m divides q, and, since m is bigger than 1, m is q. Because both m and q are prime, we can use the lemma, and, thus, H=0, so \((I+mB)^k=I\).

By applying this algorithm to all the prime divisors of k, we end up with \(mB=O_n\), so \(B=O_n\), so \(A=I\). Thus, Ker(f)={I}, so the morphism f is injective, and, consequently, bijective, so \(G\) and \(\hat G\) are isomorphic. This concludes the proof.

I can't really think of a paragraph ending this article, which is a total shame, since this problem was magnificent. I have an excuse though: I have the MAT in a few days, and I am a bit stressed out. I think I'll go play some World of Warcraft to relax. After the MAT, I will try posting more problems, though I came to realize the problems I post while under pressure are longer and harder than the normal problems I post. Maybe it's some kind of psychological mechanism behind this... I'm not foreshadowing the psychology article, btw.

Cris.

Functional Equation Involving Integrals

I'm working on a very interesting problem which I will post these days. In the meantime, here's a nice functional equation that I solved yesterday. This problem, in a changed form, was shortlisted for the 2015 Romanian NMO (National Maths Olympiad). The problem goes as follows:

Find all the functions \(f:[0,1]➝ℝ\) such that \(\int_0^x f(t)dt = f(x)^n+f(x)\), for a fixed odd n. 

Solution:

Let us consider the function \(z(x)=x^n+x\).

\(\frac{dz}{dx}=x^{n-1}+1>0\), so z is strictly increasing. It is obvious that the function is surjective, so \(z\) is bijective, and, thus, it has an inverse. Returning to the equation at hand, $$z(x)^{-1}∘(\int_0^x f(t)dt)=f(x)$$and, since the integral and z are differentiable, f is also differentiable, and, thus, continuous.

Now that we know that \(f\) is differentiable, we can differentiate the equation with respect to \(x\), obtaining that 

$$f(x)=nf(x)^{n-1}f '(x)+ \text{f '(x)   (I)} $$

Let us look now at the set \(A=[x|f([0,x])=0]\). By putting \(x=0\) in the equation, we can deduce that \(f(0)=0\), so A is not void. \(A\) is also compact, so it has a supremum, M.  By the inertia theorem, there is an interval \([M,x_0]\) such that the function keeps constant sign on that interval, with \(x_0\) being the smallest possible number with this property. If \(x_0=1\), then we have no problem. If \(x_0<1\), then it means that \(f(x_0)=0\). However, by looking at equation \((I)\), we can deduce that, if \(f(x)>0\), then \(f '(x)>0\); if \(f(x)=0\), then \(f '(x)=0\); if \(f(x)<0\), then \(f '(x)<0\). Since the sign of the function is constant on \([M,x_0]\), the function is increasing on \([M,x_0]\), and, thus, it is 0 on the interval, so \(x_0\) would be the supremum of A, which contradicts the way we chose M. This implies that the function keeps constant sign after M, and, thus, is either increasing or decreasing after M.

From now on, we shall focus on proving that \(M=1\). For the simplicity of calculations, we shall write \(f(x)=y\). If \(y>0\), then \(y'>0\). We can rearrange (I) into the form 

$$1=ny^{n-2}y'+ \frac{y'}{y}$$ 

and, by integrating, we get that 

$$\frac{n}{n-1}y^{n-1}+ln(y)-x+k=0$$

However, due to the continuity of the function, $$\lim_{x\to M}\frac{n}{n-1}f(x)^{n-1}+ln(f(x))-x+k=-∞<0$$which is a contradiction. Thus, \(f\) isn't bigger than 0, and, similarly, \(f\) isn't smaller than 0, which means that \(f(x)=0, ∀x∊[0,1]\).

The problem was quite intuitive if you think about it. It seemed pretty obvious that \(f\) can't be different than 0, but that's how most hard analysis problems are: you are asked to prove something that is intuitively correct, but incredibly hard to formalize. This exercise wasn't particularly hard, but I found it pretty instructive and rather fun. Tune in next time for an article about some isomorphism on groups of integers matrices (if I manage to learn enough Latex to make the hats (^) above classes modulo p).

Cris.

Ant on a Cube

First of all, apologies for not posting much lately. I've been really busy preparing for Olympiads/admission exams. I will probably post a lot more after the admission process is over (probably in December), but, until then, I might be a little bit inactive. As placeholders, I shall post some interesting puzzles. Here's one of them, which I took from the 2001 Oxford MAT.

A set of 12 rods, each 1 metre long, is arranged so that the rods form the edges of a cube. Two corners, A and B, are picked with AB the diagonal of a face of the cube. An ant starts at A and walks along the rods from one corner to the next, never changing direction while on any rod. The ant’s goal is to reach corner B. A path is any route taken by the ant in travelling from A to B.

(a) What is the length of the shortest path, and how many such shortest paths are there?
(b) What are the possible lengths of paths, starting at A and finishing at B, for which the ant does not visit any vertex more than once (including A and B)?
(c) How many different possible paths of greatest length are there in (b)?
(d) Can the ant travel from A to B by passing through every vertex exactly twice before arriving at B without revisting A? Give brief reasons for your answer.

Solution:

Consider the following cube in the 3D space.


The coordinates of the edges are A(0,0,0), B(1,1,0), C(1,0,0), D(0,1,0), E(0,1,1), F(1,1,1), G(1,0,1).
Let's make some quick observations. First of all, in order to get from (0,0,0) to (1,1,0), one must make an even number of steps on the \(O_z\) and an odd number of steps on \(O_x\) and \(O_y\), where a 'step' means going from one vertex to another one via the rod linking the vertexes. Thus, the total number of steps is even. The number of steps minus 1 is the number of vertexes the ant passes through. Thus, any route leading to B (a route is a collection of steps) involves an odd number of vertexes.

a) The two shortest paths are obviously A-C-B and A-D-B, each having length 2.

b) Since the ant doesn't visit each vertex more than once and the number of vertexes is 8, then it means that the maximum number of vertexes in a route is 7, because the number of vertexes must be odd. We know that the number of steps on \(O_z\) is even, so we have three cases: if the number of steps on \(O_z\) is 0, if the number of steps on \(O_z\) is 2 and if the number of steps on \(O_z\) is 4. However, there is no route with 4 steps on the \(O_z\) axis. If there was such a route, then all the 8 vertexes would be involved, because the ant can only visit each vertex once. Thus, the number of vertexes in the route would be bigger than 7, contradiction.
If the number of steps on the \(O_z\) axis is 0, then we have the routes described in a)
If the number of steps on the \(O_z\) axis is 2, then we can find the route A-H-E-D-B to be possible. This route has length 4, so 4 is a possible length. We can find the route A-H-E-F-G-C-B of length 6, too, so 6 is also a possible length. The route A-H-E-F-G-C-B passes through 7 vertexes, so 6 is the maximum length of a route.
Thus, the possible lengths are 2, 4 and 6.

c) There are 8 paths of length 6: \(A-H-E-F-G-C-B\), \(A-H-G-F-E-D-B\), \(A-C-G-F-E-D-B\), \(A-C-H-H-E-D-B\), \(A-C-G-H-E-F-B\), \(A-D-E-F-G-C-B\), \(A-D-E-H-G-F-B\), \(A-D-E-H-G-C-B\).

d) If the ant travels through each vertex other than A and B twice, then it means that it passes through 14 vertexes, which contradicts the fact that a route from A to B passes through an odd number of vertexes. Thus, such a journey is impossible.

The solution offered by the people making the MAT was similar to what I did. While solving this problem, I remembered of a problem from Thomas Povey's excellent 'Professor Povey's Perplexing Problems', which regarded the number of ways in which an ant can get from an edge of the cube to the opposing edge in a certain number of ways. I was a bit surprised to see a problem using 3D geometry in the MAT, but then I remembered that the A-level core curriculum was a lot more different in 2001 than it is now. Before that, things were even more awkward. I even encountered introductory elements of group theory in a STEP 1 from the 80's. Those times were a lot more...interesting...

Cris.

Interesting property of intersecting normal subgroups

I didn't think I'd talk about this either up until a few minutes ago.

The Romanian Maths Curriculum is extremely intriguing, mainly because of the fact that we do Analysis (at least Olympiad students do) and Linear and Abstract Algebra during our high school years. From what I've gathered, in College, we go again through these subjects in the first year, but at a more advanced level. The students who attended the Maths Olympiad during high school have a one year head-start over the ones that didn't, if you think about it, and that doesn't apply only for the Romanian Olympians who go to Universities in Romania. Participating at the Olympiad helps greatly in College, as the Olympians have more time to socialize and focus on extra-curricular activities during the first year, because they already know a lot of what the teacher is showing during the first few months. There is, however, a downside; only a few other people will have time to socialize with the Olympians, because in most Universities, there aren't a lot of people who already know a big chuck of the Curriculum.

I stumbled upon this group theory problem today, while going through a popular abstract algebra book. The problem itself, I think, is rather well known, but I discovered something that surprised me about the groups that the problem discusses.

Let \((G,*)\) be a group of order 2n, and \((H,*)\) and \((K,*)\) normal subgroups of order n such that \(H∩K={e}\). Prove that G is abelian.

Solution:

I shall prove that the only group satisfying these conditions is G={e, a, b, ab}, with \(a^2=b^2=e\), and a and b commute.

Since H and K have order n, and their intersection is e, their reunion has 2n-1 elements. Let x be the element that isn't in \(H∪K\). As a fun fact, since x isn't in \(H∪K\), \(x^{-1}\) isn't in \(H∪K\) either, because then x would be in either H or K, contradiction. Thus, \(x=x^{-1}\), so \(x^2=e\). This, however, doesn't really impact our proof. For the rest of the proof, we shall consider H* and K* as H and K minus {e}.

Let \(f_x:H^*⟶K^*\), \(f_x(h)=xh\). Obviously, this function is injective, and, since \(H^*\) and \(K^*\) have the same cardinal, it's bijective. Also, the function is well-defined, because \(xh\) can't be in H, because, if \(xh_1=h_2\), then \(x=h_2*(h_1)^{-1}\), so x would be in H.

Since the function is bijective, we have that \(xh_i=k_i\), for any i between 1 and n-1. Thus, \(x=k_i*(h_i)^{-1}=k_j*(h_j)^{-1}\), for any i and j between 1 and n-1, so \((h_i)^{-1}h_j=(k_i)^{-1}k_j\). The RHS belongs to H, and the LHS belongs to K, and we know that the only element of the intersection between H and K is e, so \(h_i=h_j=h, k_i=k_j=k\) for any i and j. Thus, H={e,h} and K={e,k}, while G is isomorphic with Klein's group: {e, h, k, hk}, and, as a fun fact, G is abelian, as required. The solution that the author of the book offered relied mostly on the fact that x has order 2, and that H and K were normal groups. The problem, as stated in the book, didn't say that H and K were normal subgroups, but rather asked you to prove that in the first part of the problem.

I've got to say, this result is a pretty intriguing property of Klein's group if you think about it. I truly hope that I didn't get anything wrong in the proof. Of course, this result pales in front of theorems such as the classification of simple finite groups, which took thousands of pages to write. However, it is a modest start. Tune in next time, for either another Analytical Geometry problem, another Probability problem, that personality article I kept talking about, or something totally random (again).

Cris.

An Old Problem from the Balkan Maths Olympiad

It was either this, or yet ANOTHER probability post. I thought of spicing things up a bit.

Here in Romania, coordinate geometry is described vaguely at the end of the 10th grade. I haven't seen exercises that involve thought in our curriculum regarding this subject, and, as an enthusiast of geometry, this saddened me, because analytic geometry is one of the stepping stones into University Mathematics. I managed to find coordinate geometry problems in MATs and STEPs, and, after a while, I managed to find one in the most prestigious Balkan competition: The Balkan Mathematical Olympiad. The problem I am about to solve is the 4th problem from the 1986 BMO. Like most other geometry problems, it has a synthetic solution, one which I will not discuss in this article. Frankly speaking, I like analytic solutions more than synthetic ones, because it gives me the rightful impression of manipulating real life objects (geometric figures) through numbers. The problem goes something like this:

The circles \(K_1\) and \(K_2\), centered at \(O_1\) and \(O_2\), with radii 1 and \(\sqrt 2\), respectively, intersect at A an B. Let C be a point on \(K_2\) such that the midpoint of AC lies on \(K_1\). Find the length of the segment AC if \(O_1 O_2 =2\).

Solution:



Let us consider \(O_1\) as the origin of the Cartesian plane, and \(O_2 (2,0)\), \(A(x_a, y_a)\), \(B(x_b, y_b)\), \(C(x_c, y_c)\).
We shall look at the triangle \(AO_1O_2\). By the cosine theorem, we have that $$(AO_1)^2+(O_1 O_2)^2-2O_1O_2 * AO_1* cos(\angle AO_1O_2) = (AO_2)^2$$Thus, \(cos (\angle AO_1O_2)=\frac{3}{4}\), and, consequently, \(sin (\angle AO_1O_2)=\frac{\sqrt 7}{4}\). We now know that \(x_a=\frac{3}{4}, y_a=\frac{\sqrt 7}{4}\). Now that we know exactly where A is, we can take a closer look at C. Let M be the midpoint of AC. Since M is on \(K_1\), and \(x_m=\frac{x_a+x_c}{2}\), \(y_m=\frac{y_a+y_c}{2}\), we can use the equation of the circle to see that \(\frac{x_{c}^2}{4}+\frac{9}{16}+\frac {3x_c}{8}+\frac{7}{64}+\frac{y_{c}^2}{4}+\frac{\sqrt {7} x_c}{8}=1\), and, thus, \(x_{c}^2+\frac{3}{2}x_c+y_{c}^2+\frac{\sqrt 7}{2}y_c=3\). By adding 1, we have that C lies on the circle with equation \((x_c+\frac{3}{4})^2+(y_c+\frac{\sqrt 7}{4})=4\) This circle has center \(O_3 (-\frac{3}{4}, -\frac{\sqrt 7}{4})\), which is the diametrically opposite point of A in regards to the circle centered in \(O_1\). It is easy to observe that A is on the circle centered in \(O_3\) with radius 2, too, so AM is the height of the triangle \(AO_{3}O_{2}\). It is easy to find the cosine of \(\angle AO_2O_3\) through the cosine theorem. $$(O_{2}C)^2+(O_2O_3)^2-2O_2O_3cos(\angle AO_2O_3)=(O_3C)^2$$and, thus, the required cosine is \(\frac{3}{4}\). Consequently, we can find \(sin(\angle AO_2O_3)=\frac {\sqrt 7}{4}\). We shall now calculate the area of \(AO_2O_3\) in two different ways. We know that $$S_{AO_3O_2}=\frac{AM*O_3O_2}{2}=\frac{AO_2*O_2O_3*sin(\angle AO_2O_3)}{2}$$
$$⟹AM=\frac{\sqrt 14}{4} ⟹ AC=\frac{\sqrt 14}{2}$$.

It was pretty surprising to find such a problem in an international Maths competition. As I said, analytic geometry isn't really discussed in the Romanian curriculum, and, from what I've seen, isn't really part of the curriculum of contests either. The thing with analytic geometry is that, at an advanced level, it's a bridge between analysis, topology and other fields of Mathematics. The importance of Geometry is obvious by looking at the Millennium Prize Problems: the Poincare conjecture. While it's proof doesn't involve Geometry per-se, its implication is partly geometrical. I have a lot of ideas for the next article, but I think that I will either write an article about Jungian psychology (new tag boys!), or I will solve a very interesting probability problem that I found in the Step 2 from last year. Or, and this one is most likely, I will decide the subject on the spot.

Cris.

The Probability of Passing a Test

Have you ever attended a test without studying anything whatsoever before it? Well your boy Cris is here to tell you something: you most certainly failed. Or, at least, you would have most certainly failed in a world fully governed by A-level Mathematics. I managed to find last year's STEP today, and I decided to take a look at some of the problems. Apart from the tedious, VERY TEDIOUS calculations, I found a nice problem that many people will emphasize with. This problem was the last Probability exercise in Step 1 last year.

A multiple-choice test consists of five questions. For each question, n answers are given
(n > 2) only one of which is correct and candidates either attempt the question by choosing
one of the n given answers or do not attempt it.
For each question attempted, candidates receive two marks for the correct answer and lose
one mark for an incorrect answer. No marks are gained or lost for questions that are not
attempted. The pass mark is five.
Candidates A, B and C don’t understand any of the questions so, for any question which
they attempt, they each choose one of the n given answers at random, independently of their
choices for any other question.
(i) Candidate A chooses in advance to attempt exactly k of the five questions, where
k = 0, 1, 2, 3, 4 or 5. Show that, in order to have the greatest probability of passing
the test, she should choose k = 4 .
(ii) Candidate B chooses at random the number of questions he will attempt, the six
possibilities being equally likely. Given that Candidate B passed the test find, in
terms of n, the probability that he attempted exactly four questions.
(iii) For each of the five questions Candidate C decides whether to attempt the question
by tossing a biased coin. The coin has a probability of \(\frac{n}{n+1}\) of showing a head, and
she attempts the question if it shows a head. Find the probability, in terms of n, that
Candidate C passes the test.

Solution:
(i) The probability of getting a correct answer to a question is \(\frac{1}{n}\). If k is smaller than 3, then the passing score isn't achieved in any scenario, so the probability of passing for k<3 is 0.
If k=3, then the probability is \(\frac{1}{n^3}\).
If k=4, then the probability of passing is \({4}\choose{3}\)\(\frac{n-1}{n^4}+\frac{1}{n^4}=\frac{4n-3}{n^4}\).
If k=5, then the probability of passing is \( {5}\choose{4}\)\(\frac{n-1}{n^5}+\frac{1}{n^5}\). In the last case, the minimum number of possible correct answers is 4, because otherwise the passing mark isn't achieved. Let us now compare the probabilities we found.
$$\frac{4n-3}{n^4}>\frac{1}{n^3}⟺4n-3>n⟺n>1$$.
$$\frac{4n-3}{n^4}>\frac{5n-4}{n^4}⟺4n^2-3n>5n-4⟺4(n-1)^2>0$$
Thus, the biggest probability of passing is when k=4.

(ii) We shall use Bayes' theorem for this one. Bayes' theorem states that, if we want to calculate the probability that the even B happens given that another event A happened before, then the probability required is \(P(B|A)=\frac{P(B⋂A)}{P(A)}\). Thus, the probability of B passing is $$P(k=4|pass)=\frac{P((k=4)⋂pass)}{P(pass)}=$$
$$=\frac {\frac{4n-3}{n^4}}{\frac{5n^2+2n-4}{n^5}}=$$
$$=\frac{4n^2-3n}{5n^2+2n-4}$$

(iii) \(P(C|pass)=\frac{10n^3}{(n+1)^5}*\frac{1}{n^3}+\frac{5n^4}{(n+1)^5}*\frac{4n-3}{n^4}+\frac{n^5*(5n-4)}{n^{5}*(n+1)^{5}}=\frac{25n-9}{(n+1)^5}\).

The problem itself was rather easy, and the calculations were simple enough to be done quick enough. The Step this year had some really interesting geometry problems, and, from what I've heard, had a monster algebra problem. While I find Step questions insanely interesting, I find the calculations required a bit tedious.

I attended a contest similar to the one described in the problem when I was younger. I am pretty sure many kids across the world, too, participated at the Mathematical Kangaroo competition. It was a rather good mental exercise for kids, in which you were asked to solve 30 questions in an hour and a half or something. I never did good in multiple choice tests, so I didn't have insanely good results at it; if I recall correctly, I once started crying desperately in one such contest, and the teacher assisting us was afraid to take my paper when the time concluded. Yikes!

Cris.

An application of Complex Algebra in Geometry

A few days ago, I wrote about posting my favorite problem. The thing about this problem is that it's extremely simple through synthetic geometry, but I found a way of solving it using complex numbers in a way that baffled me. It took 3 pages to solve this problem in my 'Notebook of Nice Problems' (which we shall call NNP from now on; I might even add a tag for problems I took from there). Some people have called me sadistic for liking this type of solutions, but I took it as a compliment. Without further ado, let's get right into the problem!

Let ABC be a triangle with AD as a bisector and AM as a median, with D and M laying on the line BC. Let P be a random point on AD, and E and F the projections of P on the lines AB and AC. If K is the intersection between EF and AM, prove that PK is perpendicular on BC.



First of all, we shall presume that ABC is not isosceles with AB=AC. If ABC is isosceles with AB=AC, then AD and AM coincide, and PK is obviously perpendicular on DC.

Let us use the transversal theorem in the triangle ABC. We shall consider the transversal E-K-F, and the line denoted by A-K-M, which passes through K. Thus, we get that $$BM \frac{FC}{FA} + MC \frac{EB}{EA} = BC \frac{KM}{KA}$$However, \(AM=MC=\frac{BC}{2}\), so we get that $$\frac{FC}{FA}+\frac{EB}{EA}=2\frac{KM}{KA}$$We shall call this relation (1). By using the property of points on the bisector, we get that \(PE=PF\), and, by triangle congruences, \(AE=AF\). Thus, (1) transforms into \( \frac{FC+EB}{2EA}=\frac{KM}{KA}\). However, \(FC=AC-AF\), and \(EB=AB-AE\), so the relation transforms further into \( \frac{AB+AC}{2EA} -1=\frac{KM}{KA}=r\).

Let us center the complex plane in A. By using the usual notations and by considering AB as the real positive axis, we have that \(e,b⋲R_{+}^*\). We can write \(k=\frac{m+r*a}{1+r}=\frac{m}{1+r}=\frac{b+c}{2(1+r)}\) (2)

Since \( PE⟘AB, PF⟘AC, PE=PF\), it follows that \(\frac{e-p}{b}⋲iR, \frac{f-p}{c}⋲iR, |e-p|=|f-p|\). $$\frac{e-p}{b}⋲iR ⟺ \frac{e-p}{b}=\frac{p^{*}-e^{*}}{b^{*}},$$where \(x^{*}\) is the conjugate of \(x\). $$⟹eb^{*}+e^{*}b=pb^{*}+p^{*}b$$
Similarly, we get that $$fc^{*}+f^{*}c=pc^{*}+p^{*}c$$We shall call these relations (3) and (4) respectively. Apologies for not being able to write the relations next to the equations, I still have to work on my Mathjax skills. I will (probably) learn how to fix this problem in the (far) future. If \(w=cosA+isinA ⟹ f=ew\). \(PK⟘BC ⟺\frac{k-p}{c-b}=\frac{p^{*}-k^{*}}{c^{*}-b^{*}}\).
$$⟺kc^{*}-pc^{*}-kb^{*}+pb^{*}=p^{*}c-ck^{*}-p^{*}b+bk^{*}$$
$$⟺kc^{*}+k^{*}c-bk^{*}-b^{*}k=p^{*}c+c^{*}p-p^{*}b-pb^{*}$$
$$⟺kc^{*}+k^{*}c-k^{*}b-kb^{*}=fc^{*}+f^{*}c-eb^{*}-e^{*}b$$The last line is obtained from combining (3) and (4), and we shall call it (5). Let us replace k as we obtained it in (2). Let us also remember that e and b are positive numbers, so they are equal to their conjugate and modulus.

$$⟹ (5) ⟺ \frac{(b+c)c^{*}}{2(1+r)}+\frac{(b^{*}+c^{*})c}{2(1+r)}-$$
$$-\frac{(b^{*}+c^{*})b}{2(1+r)}-\frac{(b+c)b^{*}}{2(1+r)}=ewc^{*}+ew^{*}c-eb^{*}-e^{*}b$$
$$⟺\frac{|c|^2-|b|^2|}{1+r}=ewc^{*}+ew^{*}c-eb-e^{*}b,$$which shall be known from now on as (6). Let us remember that \(\frac{AB+AC}{2EA}=1+r ⟹\frac{|b|+|c|}{2|e|}=1+r.\)
$$⟹ (6) ⟺ \frac{2e(|c|-|b|)(|c|+|b|)}{|b|+|c|}=ewc^{*}+ew^{*}c-eb-e^{*}b$$
$$⟺ 2(|c|-|b|)=cw^{*}+w^{*}c-2b$$
This shall be known as (7). However, \(c=\frac{w|c|b}{|b|}\).
$$⟹(7)⟺2(|c|-|b|)=ww^{*}b^{*}\frac{|c|}{|b|}+ww^{*}b\frac{|c|}{|b|}-2b$$
$$⟺2(|c|-|b|)=2b\frac{|c|-|b|}{|b|} ⟺ 2=2$$
The last line is true, because |c| is different than |b|, as AB is different than AC. Thus, \(PK⟘BC\) 𞺑

Writing that square at the end of this proof feels so satisfying. The calculations were very tedious when I first solved the problem, but I enjoyed it nonetheless. Of course, in the actual context of Mathematics, this proof isn't hard, but it's a nice exercise for anyone with basic knowledge of complex numbers and with a bit of imagination regarding Geometry.

P.S: This will be the last template update for a while, as I pretty much like this layout of the blog.

Cris.

Property of real skew symmetric matrices

If you don't know what a skew-symmetric matrix is, don't worry; I didn't know what it meant either until I found this problem. It's literally a matrix A for which \(A^T=-A\). In this article, we have to prove that the rank of any real skew symmetric matrix is even. From what I've been told, the rank of any skew symmetric matrix, in any field with characteristic different than 2, is even, but for now I only know how to prove this property for the \(M_n {(R)}\). Without further ado, let's get straight into the problem.

First of all, let us prove a few lemmas:

1. If A is a real skew symmetric matrix, then it is diagonalizable.

Through Schur's theorem, we see that there is a matrix \(S\) in \(M_n (R)\) that satisfies the following properties: \(SS^{T} = I_n\) and \(SAS^{-1} = J\), where J is an upper triangular matrix. By writing \(S^{-1}=S^{T}\) and the same relation with S, we have that \(-(S^{-1})^{T}A^{T}S^{T}=-J^{T}\), and \(J^{T}\) is a lower triangular matrix. J is a diagonal matrix, because the entries under the diagonal, 0s, are equal to the negatives of the values above the diagonal. Thus, A is diagonalizable.

2. The eigenvalues of a real skew symmetric matrix are either pairs of complex conjugates or 0.

If \(\lambda\) is an eigenvalue of A, then \(AX=\lambda X\), for a certain vector X. By transposing, we get that \(X^{T}A^{T}=\lambda X^{T}\). Conjugate the whole thing, then multiply to the right by \(X\) and replace \(A^{T} = -A\) and \(AX=\lambda X\), and you get that \(\lambda\) is a purely imaginary number or 0. In order to prove that the conjugates are eigenvalues too, we just look at the characteristic polynomial of A is \(\lambda\), and conjugate it. Since A is real, it's characteristic polynomial has real coefficients, so the conjugate of \(\lambda\) is also a root.

Now we are ready to solve the problem. Since A is diagonalizable, then there exists an S such that \(SAS^{-1}=J\), where J is the Jordan canonical form of A. Since the eigenvalues of A come in pairs of conjugates, the rank of A is equal to 2 times the number of non-zero eigenvalues, so it is even.

As with most matrix problems that use this theory, they are somewhere on the boundary between college Mathematics and high school Mathematics. As far as I know, the high school curriculum doesn't include Jordan forms or Schur's theorem in any country (perhaps except for some countries in Asia). Apologies for the fact that this article is a bit smaller, but I've got something really interesting on the way; one of my all time favorite problems is coming in the next article.

Cris.

Benford's Generalized Law

First of all, apologies for my lack of posts recently; school started for me, so I don't really have time for much. I have been working on an article regarding the Hollow Earth theory in which I debunked it, but, after writing the article, I realized that I made a mistake somewhere along the way, and, frankly speaking, I rage-quited. I still wanted to write an article, so I took out my 'notebook with notable problems' (I have one of those, I'm a full-time nerd), and I came across the Newcomb-Benford law, which states that the numerical values of the vast majority of social phenomena (the majority modeled by exponential evolutions in rapport to time) start with 1. The law takes its name from its two discoverers, Frank Benford, who wrote about it in 1938, and Simon Newcomb, who discovered it in 1881. Both discovered it independently from one another.  This problem was also proposed in a Gazeta Matematica back in February 2017.

Let \(f(t)=a^t\) be the function modeling a specific social event. We are looking at the values of t for which $$10^n<f(t)<2*10^n$$. By taking logarithms, we get that \( n<t log(a)<lg2 + n\). Thus, the probability that the first digit of f is 1 is log2, which is roughly equal to 0.301. For the general case, $$lg(d)+n<t lg(a)<lg(d+1)+n$$,where d is the first digit of f, so the probability that the first digit is d is equal to \(log(d+1)-log(d)\). The function \(log(x+1)-log(x)\) is decreasing for all positive x, so the probability of each digit appearing is decreasing. Obviously, the law works for all numerical bases.

We can also do a quick generalization of this result. How about we derive the n-th digit of an exponential function? Let us presume that the exponential function has m digits, with m bigger than n. Now, we know that \((10M+d)*10^{m+1-n}<a^t<(10M+d+1)*10^{m+1-n}\), where M is the number composed by the first n-1 digits. Thus, by taking logs again, we get that $$(m+1-n)log(10M+d)<tloga<(m+1-n)log(10M+d+1)$$, so the required probability, for a certain M, is \(log(1+ \frac {1}{10M+d})\). Since M is the number made by the first n-1 digits, it takes values from \( 10^{n-2}\) to \(10^{n-1}-1\), so the required probability is $$P(d)= \sum_{k=10^{n-2}}^{10^{n-1}-1} log(1+ \frac {1}{10k+d})$$.

After doing a quick search on Wikipedia, I found out that this result has some practical uses. Apparently, price digits and election results can be somehow checked by this law, and it appears to have applications in molecular genetics, too. Perhaps some old results like this are still revolutionary to this day.

Cris.

Making a tour of a square grid

The new design update of the blog deserves a content update too, don't you think? This problem is part of the 'Intriguing Puzzles' series, which I will post from time to time.

This specific puzzle is rather well known, and I am sure that most people may recognize this. There are lots of puzzles regarding 'tours' of certain buildings; by tour, I mean going through each room only once and then returning to the starting room. There is a problem, however: not all buildings can be toured. For this puzzle, we will consider a nxn rectangular grid. Let us look at a 5x5 grid.

We shall prove that such rectangular grids can't be toured. I came across this problem in the Oxford Mathematics Aptitude Test from 2009, yet I am sure that it was posed many times before.

By absurd, we shall presume that the grid can be toured.

Let us color the rectangular grid in black and white like a chessboard:



A 'move' is defined as the movement from one room to a neighboring room. Let us observe that, if a tour starts in a room of a certain color, it takes an even number of moves to return to a room of the same color. A tour of a grid should consist as \(n^2\) moves, as that's the number of rooms you need to tour. In the case of an odd n, the number of rooms is odd, so the number of moves is odd. Thus, after \(n^2\) moves, you can't return to a room of the same color as that of the room you started from, resulting in a contradiction.

The problem given by Oxford was more complicated than this; this was the last part of the problem given at Oxford. In the first four parts, you had to deal with a rectangular \(n*n\) grid with an even n. This problem reminds me of a puzzle regarding covering a chessboard with dominoes because of the strategy used. But that's a puzzle for another time.

Cris.

Solar System's Escape Velocity

This is a step-up from the previous post about the Earth's escape velocity, though this one won't be as exact as the one before. The Solar System is a lot more complicated than what I am about to do, but it's a pretty nice challenge for anyone interested in problems regarding gravity. We shall consider the problem as it was asked by Thomas Povey in his 'Professor Povey's Perplexing Problems' book: only the Sun and Earth affect the escape velocity. Let us calculate the escape velocity from the Solar System, in the reference frame of the Earth's surface. Let \(\alpha\) be the angle at which a probe is sent outside of the Solar System.

First off, a few conventions: the distance between the Sun and the Earth is 149.6 million kilometers, the radius of the sun is 695,508 kilometers, the mass of the sun is \(2*10^{30}\) kilograms, the mass of the Earth is \(6*10^{24}\) kilograms, and the radius of the Earth is 6,371 kilograms, and the gravitational constant G is \(6.6*10^{-11} \frac {N m^2}{kg^2}\).

Let's take a look at the following drawing:



Let S be the center of the Sun, E the center of the Earth. Let the vector CD be the direction our probe is sent outside the Solar System. In order to find the required speed, we first need to find the speed at which the Earth rotates around its own axis, and the speed at which the Earth rotates around the Sun.

$$V_E=W_E R_E$$, where \(W_E\) is the angular velocity of the Earth around its own axis. We know the frequency at which the Earth rotates, the inverse of the number of seconds in a day, \(\frac {1}{86400}\) seconds. Thus, \(W_E = \frac {2\pi}{86400} rad*s^{-1}\). Through an easy calculation, we get that \(V_E=0.47 \frac {km}{s}\).

Now for the speed around the Sun. The frequency of a rotation is \(\frac {1}{86400*365}=\frac {1}{31536000}\). The speed at which the Earth rotates around the sun is \(V_{ES}=W_{ES}R_{ES}\), which is approximately \(30 \frac {m}{s}\).

The next part of the question is to figure out the work required to leave the Solar System. This work is equal to the sum of the work required to escape the Earth and the work required to escape the Sun. Thus, this work is $$W=\int_{R_E}^{\infty} \frac {G M_E m}{r^2} dr + \int_{R_{ES}}^{\infty} \frac {G M_{ES} m}{r^2} dr = \frac {GM_E m}{R_E} + \frac {GM_S m}{R_{ES}}$$. This work must be equal to the kinetic energy, so $$ \frac {GM_E m}{R_E} + \frac {GM_S m}{R_{ES}} = \frac {mv^2}{2}$$

Thus, $$v=\sqrt{2G(\frac {M_E}{R_E} + \frac{M_{S}}{R_{ES}})}=43.67 \frac {m}{s}$$.

Let \(v_i = V_{ES}+V_E = 30.47 \frac {km}{s}\). This is the modulus of the vector \(\vec{CD}\). The escape velocity is the modulus of the difference between the vectors \(\vec{EB}\) and \(\vec{CD}\), where the modulus of EB is \(v\). Let us decompose \(\vec{v_i}\) on the \(O_x\) and \(O_y\) axis. \(\vec{v_i} = v_i cos(\alpha) \vec{i} + v_i sin(\alpha) \vec{j}\). Thus, the required speed is $$v_{esc}=|\vec{v}-\vec{v_i}|=\sqrt {(v - v_i cos(\alpha))^2 + (-v_i sin(\alpha))^2}=$$
$$=\sqrt { v^2-2v*v_i sin (\alpha) +(v_i)^2}$$.

As a small observation, the smallest escape speed is when \(\alpha = \frac {\pi}{2}\), which is equal to roughly 13.2 kilometers per second, while the largest escape speed is when \(\alpha=- \frac{\pi}{2}\), and is roughly equal to 74.2 kilometers per second. The direction is highly important when launching satellites, as can be seen by the given calculations.

It would be fun to find the escape velocity of the Galaxy as the generalization. I did a quick research, and, apparently, the escape velocity of the Galaxy is 537 kilometers per second. That's about 2,073,600 kilometers per hour. For comparison, the fastest man-made object ever is the spacecraft Helios 2, which, in 1989, was moving away from the Earth at a speed of 356,040 kilometers per hour. It's going to take a long while before we leave the Galaxy.

Cris.

Nice Step 2 Probability Question

As you may have noticed, I am an enthusiast of anything mathematical. Applying mathematics in something from the natural world is a pretty intriguing idea to me, even though I haven't really studied Physics as much as I should have during high school. The closest I can come to something 'real' by doing Maths is through Probability questions. While most questions revolve around random variables and probabilities regarding those, there are some questions which revolve around easy-to-understand events. Here's one of those problems, which I found in the 2011 Step 2 (one of the exams needed to get admitted to Cambridge).

Xavier and Younis (pretty weird names) are playing a match. The match consists of a series of games and each game consists of three points. Xavier has probability p and Younis has probability 1-p of winning the first point of any game. In the second and third points of each game, the player who won the previous point has probability p and the player who lost the previous point has probability 1-p of winning the point. If a player wins two consecutive points in a single game, the match ends and that player has won; otherwise,the match continues with another game.

a) Let w be the probability that Younis wins the match. Show that for p different than 0, $$w=\frac {1-p^2}{2-p}$$. Show that \(w>1/2\) if \(p<1/2\), and \(w<1/2\) if \(p>1/2\). Does w increase whenever p decreases?

This is the longest part of the problem. Let us analyze what happens during each game through a probability tree.


In the image above, Y stands for Younis winning a point and X stands for Xavier winning a point. It is easy to say that the probability of  Younis winning is $$p-p^2+p(p-p^2)=p-p^3$$. The probability of neither winning nor losing is $$(1-p)^3+p(1-p)^2=(1-p)^2$$.

The probability of Younis winning the first game is the probability above, \(p-p^3\). For Younis to win in the second match, the first match must conclude in a draw, and, thus, the probability of Younis winning in the second match \((1-p)^2 (p-p^3)\). Thus, the probability of Younis winning is an infinite sum: $$w=(p-p^3)\sum_{n=1}^{\infty}(1-p)^{2n}=\frac {1-p^2}{2-p}$$

By differentiating in rapport to p, \(\frac {dw}{dp} = \frac {p^2-4p+1}{(2-p)^2}\), which is bigger than 0 if \(p^2-4p+1>0\), which happens if p isn't in the interval between \(2-3^{1/2}\)and \(2+3^{1/2}\). Since the first fraction is smaller than 0.5 and the latter is bigger than 0.5, it means that \(w\)is decreasing in 0.5, and \(w(0.5)=0.5\), so the conclusion of the problem holds.

b) If Xavier wins the match, Younis gives him 1 pound; if Younis wins the match, Xavier gives him k pounds. Find the value of k for which the game is 'fair' in the case when p=2/3.

It is easy to say that Younis' expected profit is \(w\) pounds, while Xavier's expected profit is \((1-w)k\). $$w(2/3)=\frac {5}{12}, (1-w)k=\frac {7}{12}k=\frac {5}{12}$$, so \(k=\frac {5}{7}\)pounds.

c) What happens if \(p=0\)?

If \(p=0\), then Younis will win the first and last points in each game, and Xavier will win the second point; thus, the game never ends, as no one will win two consecutive games.

It is pretty hard to come across elementary Probability problems, even in undergraduate exam papers. I pretty much enjoy this type of problems, as it challenges the student to think about a (more or less) real situation and apply probability in it. This problem was rather easy, yet it was pretty fun to solve, at least for me. Tune in next time for who-knows-what type of problem.

Cris.

Earth's escape velocity

You'd be surprised how many intriguing Physics results are on the borderline between high school Maths and College Maths. This one is one of my favorites, mainly because it is actually applied (probably) in rocket science and it gives the feeling of greatness to anyone calculating/understanding it.

Before we start, let me give you some formulas:
The force of attraction between two bodies of masses M and m respectively, with a distance R between their center of masses, is $$F=\frac{GMm}{R^2}$$ (I actually managed to properly write fractions!)
G is the constant of gravitation, which is roughly equal to \(6.7*10^{-11} Nkg^{-2}m^2\). The mass of the Earth is \(5.972*10^{24}kg\), but, to make the job of the calculator easier, we shall use \(6*10^{24}kg\). The radius of the Earth is \(6,4*10^{6}m\). Now that we know these formulas, we can get to the task at hand.

The net force required to leave the Earth is, obviously, equal to the attraction force. Because an object is incredibly small compared to the radius of a planet, we shall consider the distance between the object and planet equal to the radius of the planet.

In order to leave the planet, one must exert work with distance reaching infinity, and, thus, the work needed to escape the planet is $$\int_R^⧞ \frac {MmG}{R^2} dr=\frac {MmG}{R}=\frac{mv^2}{2}$$.

Thus, we get that \(v^2=\frac {2MG}{R}\), so \(v={(2MG)^{1/2}}{R^{1/2}}\). By plugging in the mentioned constants, we get that the speed is about 11.20825 kilometers per second. That's roughly 40338 kilometers per hour.

You'd think that such a speed can be achieved only by incredibly complex pieces of technology with highly complex engines and complicated patterns, yet the first object to reach escape velocity is a steel plate covering a nuclear test back in 1957. It is unknown if it did actually leave Earth's atmosphere, as it would have probably boiled due to the high speed, but one thing is sure: no one found its debris. Who knows, maybe the first man-made creation the aliens find won't be one of the Voyager probes, but rather a random steel plate floating randomly through the Solar System.

Cris.

Old Topology Problem

'Gazeta Matematica', the most widely known Mathematical journal in Romania, begins its year by publishing problems from old years ending in the same digit as the year that just started. This year, they published problems from years ending in 8. The problem that I am about to share was published in 1968 by T. Zamfirescu, and is solvable through Helly's theorem. Without further ado, let's get straight into the problem.

Let d be a line in space and S a finite set of spheres such that any 3 spheres have an interior point in common. Prove that there exists a line d' parallel to d that intersects all the spheres.

Helly's theorem in a plane states that if a finite number of convex sets with the property that any three convex sets intersect, then all convex sets intersect.

Here's the proof of the theorem: Let m be smaller or equal to n, where m is the maximum number of sets with the intersection I different than the empty set and let us presume by absurd that \(m<n\), so there is C such that C doesn't intersect with I. Because C and I are convex sets, there must be a line d that separates them, they are in planes \(S_1\) and \(S_2\) respectively. Because \(m>2\), we need at least 3 sets to create I. Let \(C_1\) and \(C_2\) be two of them. Obviously, I is included in them. From the hypothesis, \(C_1\), \(C_2\) and C intersect. We choose the point A in their intersection and the point B in I. Thus, A is in \(S_1\) and B is in \(S_2\). Since A and B are in \(C_1\) and \(C_2\), the whole segment AB is in \(C_1\) and \(C_2\), and, thus, AB and d intersect. We now have that for any sets \(C_1\) and \(C_2\) that contain I, the intersection between \(C_1, C_2\) and d is not the empty set. By writing in a different form, we have that the intersection between \(C_1\) and d intersects with the intersection between $C_2$ and d. Thus, by considering the intersections as segments, we have m segments on a line such that each pair of segments intersects. By Helly's theorem on a line, we have that all the m segments intersect, so, by writing the intersection of the segments as the intersection of \(C_i\)-s and d, we have that I intersects with d, which is a contradiction. Thus, m=n.

Back to the problem at hand, let us consider a plane P such that d is perpendicular on P. Now, let us project the spheres on P. We get a set of circles with the property that any 3 of them intersect, and, thus, from Helly's theorem in a plane, we get that the circles intersect. Since the spheres intersect in an interior point, the circles have an actual surface in common, not only a point. Let A be a point in that surface. The line through A that is parallel to d is the required d'.

Of course, this problem isn't a hard topology problem, but it is pretty hard for the undergraduate level.

This article wasn't the different article that I promised. That one is still underway. Stay tuned folks, more problems/journals/randomness is coming.

Cris.

Matrix solvable through Jordan form

One of the worst experiences (and failures) of my life was the National Maths Olympiad from the 11th grade. It was a traumatizing experience, since the Olympiad took place in a remote part of the country (I come from Romania), and the subjects were incredibly hard. I managed to win a bronze medal, though I was very disappointed with myself. A month ago, I gathered my strength and looked through the shortlist for the Olympiad. The problem I am about to solve was the only linear algebra problem in the shortlist, and, just like the one from the Olympiad, it is solvable through the Jordan canonical form. The Jordan form wasn't part of the syllabus of the Olympiad, which was a dirty move from the problem selection committee. Nonetheless, I was inspired by this experience, and, in the meantime, I studied the canonical form.

Without further ado, let's get straight into the problem.

Let A be an \(n x n\) matrix with complex entries. Prove that \(A^2=O_{n}\) if and only if there are complex \(n x n\) matrices B and C such that \(A = BC\) and \(CB=O_{n}\).

I will post the matrices as photos, because posting them in Latex is tedious.

Let 1) be \(A^2=O_{n} => B, C\), and 2) be \(B, C => A^2=O_{n}\).

2) => 1)

$$A=BC, CB=O_{n}$$

$$A^2=B(CB)C=O_{n}$$

The next one will be 'slightly' longer.

1) => 2)

\(A^2=O_{n}\) Thus, the minimal polynomial of A divides \(X^2\).

1. The minimal polynomial of A is X, so \(A=O_{n}, B=O_{n}\), while C is any random matrix.

2. The minimal polynomial is \(X^2\)

We shall start using the Jordan canonical form. We know that the maximum order of any Jordan block corresponding to a specific eigenvalue is equal to the number of apparitions of \(X-a\) (where a is an eigenvalue) in the minimal polynomial. Thus, the maximum order of a Jordan cell is 2, and the Jordan canonical form of A looks something like this:

Everything above the J-s and 0-s is 0. The J-s look something like this:

We shall be looking for matrices B' and C' such that \(B' C' = J\) and \(C' B' = O_{n}\)

Let us write B' and C' in the form

   , .

We need to find \(B_{i}\) and \(C_{i}\) such that \(B_{i} C_{i} = J_{i}\) and $$C_{i} B_{i} = O_{n}$$. The perfect example of such matrices is \(B_{i}=J_{i}\) and \(C_{i}\) of the form

With \(B_{i}\) and \(C_{i}\) found, we can write B' and C'. 

Let S be a matrix such that \(SAS^{-1} = J\). Thus, \(S^{-1}JS=A\), and \(S^{-1}B' C' S=A\). We can take \(B=S^{-1}B'\), and \(C=C'S\). Thus, \(BC=A\) and \(CB=C'SS^{-1}B'=C'B'=O_{n}\), so there exist B and C, which concludes the problem.

It was very interesting to solve a problem with the Jordan canonical form, as the methods used aren't very common in high school Mathematics. The problem itself wasn't extremely difficult, yet it was interesting nonetheless. Tune in next time for an article that might be about something rather...different.

Cris.

                                                                                                                  

                                                                                                                  

Gamer's Journal #2

Hello there! Today on our second release of Gamer's Journal I am going to present you the specs of the new Ray-Tracing Geforce RTX Lineup from NVidia , featuring the RTX 2070 , RTX 2080 , RTX 2080Ti .

Here you will find the specs of them , and the cost as well :

Geforce RTX 2070 FE Specs & Price : 

 -NVIDIA CUDA Cores : 2304

 -RTX-OPS : 45T 

 -Giga Rays : 6

 -Boost Clock [MHz]: 1710(OC) 

 -Base Clock [MHz]: 1410 

 -Standart Memory Config : 8GB GDDR6

 -Memory Speed : 14 Gbps

 -Memory Interface Width : 256-bit

 -Memory Bandwidth : 448 GB/s 

 -Standard Display Connectors : DisplayPort , HDMI , USB Type-C ,DVI-DL

 -Graphics Card Power [W] : 185W

 -Supplementary Power Connectors : 8 pin

 -Price : $ 599.00

Geforce RTX 2080 FE Specs & Price :

 -NVIDIA CUDA Cores : 2944

 -RTX-OPS : 60T

 -Giga Rays : 8 

 -Boost Clock [MHz] : 1800(OC)

 -Base Clock [MHz] : 1515

 -Standart Memory Config : 8GB GDDR6

 -Memory Speed : 14 Gbps

 -Memory Interface Width : 256-bit

 -Memory Bandwidth : 448 GB/s

 -Standard Display Connectors : DisplayPort, HDMI, USB Type-C

 -Graphics Card Power [W]: 225W

 -Supplementary Power Connectors : 6 pin + 8 pin

 -Price : $ 799.00

Geforce RTX 2080Ti FE Specs & Price : 
 -NVIDIA CUDA Cores : 4352
 -RTX-OPS : 78T
 -Giga Rays : 10
 -Boost Clock [MHz] : 1635(OC)
 -Base Clock [MHz] : 1350
 -Standart Memory Config : 11 GB GDDR6
 -Memory Speed : 14 Gbps
 -Memory Interface Width : 352-bit
 -Memory Bandwidth : 616 GB/s
 -Standard Display Connectors : DisplayPort, HDMI, USB Type-C
 -Graphics Card Power [W] : 260W
 -Supplementary Power Connectors : 8 pin + 8 pin
 -Price : $ 1,199.00

These GPUs are using Ray Tracing , which is a new technology ( and the definitive solution ) for lifelike lighting , reflections , and shadows , offering a level of realism far beyond what's possible using traditional rendering techniques .

These new Turing GPUs feature new advanced shading technologies that are more powerful, flexible, and effiecient than ever before. Combined with the world's fastest memory - GDDR6 - this performance lets your rip and tear through games with maxed-out settings and incrediibly high frame rates .

 Note that they won't be compatible with current SLI Bridges , so you will have to buy the new Geforce RTX NVLink Bridge .

These specs are taken from NVidia's Official Site , so no scammerino 

In the next Gamer's Journal , I am going to talk about a video game that combines 2 major industries : Gaming and PC Components ! Stay tuned to find out

Gamer's Journal #1

Here on Gamer's Journal , you are going to find info about new Computer Components , as well peripherials , but most importantly , info about new video games !

So , without further ado , let's get to the main info about your next PC upgrade! Intel gave us earlier this day an opportunity to preorder their new 9th gen Skylake-S CPU's .

Here are the specs of them  : 

 Core i9-9900K : It is going to have 8 processing cores and 16 threads , it has a base clock of 3.6 GHz (It can be further overclocked up to 5.0 GHz on one or 2 cores) , and 16 MB of Intel Smart Cache . It draws about 95W from the PSU , and it comes at a cost of 450 USD .

Core i7-9700K : It is going to have the same number of cores as the i9 , but half the amount of threads . It has a base clock of 3.6 GHz , same as the core i9 (It can be further overclocked up to 4.9 GHz on 1 core) . It has 12 MB of Intel Smart Cache , and draws about 95W from the PSU , coming at a cost of no more than 350 USD . 

Core i5-9600K : It is going to have 6 cores and 6 threads , and it is gonna have a base clock of 3.7 GHz (It can be further overclocked up to 4.6 GHz on 1 core) . It has 9 MB of Intel Smart Cache , and draws about 95W from the PSU . It comes at a reduced cost of about 100 USD than its 8th gen brother , being about 250 USD . 

Keep in mind that these Skylake-S CPUs are compatible with curent Z370 Chipset Motherboards , but they can be fully operational on a new motherboard with a new Z390 Chipset . 

Note that all the specs given above are official , so no scammerino 

In the next Gamer's Journal , I am going to talk about NVidia's new Ray-Tracing RTX 2070 , 2080 , 2080Ti , so stay tuned !!

Signed by Papa Radu

             

Our newest member

The Science Blog is pleased to welcome our new member, Lightwall AKA Radu AKA my cousin! He is an enthusiast of anything technological, and he will write interesting articles regarding computers, while also coordinating the Gamer's Journal, which will contain info about all sorts of things that will surely benefit any gamer. He's also a pro gamer, his favorite games being DOOM, CoD and Rocket League. I hope you'll enjoy his articles!

Cris.

   

An interesting puzzle in probability (which has almost nothing to do with probability)

When I was younger, sometime during the 4th grade or so, I had this subject at school called 'Funny Mathematics' (quite informal for a school subject). I was quite intrigued by it during the summer before 4th grade, mainly because I had no idea what it would involve. I had high expectations from it, but was disappointed when the school year started and we got our manuals. After going through the 'Funny Mathematics' manual, I found out that it contained some sort of brain teasers ('If Mary's dad has 3 daughters, 2 of which are called May and August, what is the name of the 3rd one' and other variations of this question) and some puzzles with sticks (the typical 'move the sticks so that the resulting operation is correct' questions). Let me just say, I never found that type of Mathematics to be funny. However, earlier this year, I came across Martin Gardner's 'Colossal Book of Short Puzzles and Problems', which contained a lot of intriguing problems that reminded me that funny mathematics actually exists. One of them, proposed in the Probability chapter, goes as follows:

'A man arrives at a random spot several miles from the Pentagon. He looks at the building through binoculars. What is the probability that he will see three of its sides?'

The fact that he watches through binoculars implies that we don't have to deal with the limitation of eyesight; we can presume, for the sake of this problem, that the man can see the Pentagon from a point infinitely far from the Pentagon.

I will present two solutions, one trivial (the solution proposed in the book; sadly, I didn't think of it), and my solution, involving calculus.



First solution:

Let us drawn the Pentagon and call it ABCDE. By intersecting the sides of the Pentagon, we can denote the areas in which the observer can see 1, 2 or 3 sides.

The drawing above shows the areas for which the observer sees 1, 2 and, respectively, 3 faces of the pentagon. Let us observe that, if the observer stays in a 2-area, then the symmetric of the observer through the center of the Pentagon, then the symmetric of the observer has an infinitely small chance of lying in the 1-area and a probability of being in a 3-area. Thus, the probability of the observer seeing 3 sides is the same as the probability of the observer seeing 2 sides, and the probability that the observer sees 1 side tends towards 0. Thus, \(P(1)+P(2)+P(3)=2P(3)=1\), so \(P(3)=1/2\).

Sadly, as I said, I couldn't see this solution when I solved the problem. Let me show you my solution.

Second solution:



We shall keep the notations we used during the last solution. Since all the 2-areas and 3-areas are the same, we shall only look at one pair of such areas: The 3-area denoted by ED and AB, and the 2 area denoted by DC and AB. On the line DC, let us take the point $K_1$. Let \(L_1\) be the intersection of the line parallel to GI drawn through \(K_1\), and let \(M_1\) be a point on ED such that \(IL_1=IM_1\). Obviously, \(GIL_{1}K_{1}\) is an isosceles trapezium. Let \(x=GK_1\). The area of the trapezium \(GIL_{1}K_{1}\) is

\(A_{1}(x)=((GI+K_{1}L{1})/2)*h_{1}(x)\).

Since ABCDE is a regular pentagon, its angles are all equal to 108 degrees. After doing some angle chasing, we can deduce that the angles in \(GIL_{1}K_{1}\) are 108 degrees and 72 degrees.

$$K_{1}L_{1}=GI+2x*cos(18)$$

Thus,

$$A_{1}(x)=((2GI+2x*sin(18))/2)*(x cos(18))$$
$$=GI*xcos(18)+x^{2}*(sin(36)/2)$$

, and the area of \(IL_{1}M_{1}\), which is \(A_{2}(x)\), is equal to

$$A_{2}(x)=(x^{2}*sin(36))/2$$

Thus, $$[A_{1}(x))/(A_{2}(x)] = [GI*xcos(18)+x^{2}*(sin(36)/2)]/[x^{2}*(sin(36)/2)]$$. It is easy to observe that

$$\lim_{x\rightarrow infinity}\ (A_{1}(x)/A_{2}(x))=1$$, and, thus, the probability that the observer sees 3 sides is the limit towards infinity of \((A_{1})/(A_{1}+A_{2}+C)\), where C is the constant sum of the 1-areas and the small triangles in the 2-areas that weren't part of \(A_{2}(x)\).

This problem was really interesting to solve, and I pretty much enjoyed the fact that it could be solved through calculus. I am a geometry enthusiast, and combining geometry with ANYTHING else is amazing. 

Ion Barbu, one of the great Romanian intellectuals (he was both a Mathematician and a Poet), once said that, and I quote, 'as contradictory as these subjects might be at first sight, there is, somewhere, in the higher planes of geometry, a place where it meets poetry.' I tend to agree with him, to be honest. I believe that the higher planes of geometry (I love this expression, it's kind of pun-y) intersect with many other fields of study, which I am eager to explore.

Cris.