A set of 12 rods, each 1 metre long, is arranged so that the rods form the edges of a cube. Two corners, A and B, are picked with AB the diagonal of a face of the cube. An ant starts at A and walks along the rods from one corner to the next, never changing direction while on any rod. The ant’s goal is to reach corner B. A path is any route taken by the ant in travelling from A to B.
(a) What is the length of the shortest path, and how many such shortest paths are there?
(b) What are the possible lengths of paths, starting at A and finishing at B, for which the ant does not visit any vertex more than once (including A and B)?
(c) How many different possible paths of greatest length are there in (b)?
(d) Can the ant travel from A to B by passing through every vertex exactly twice before arriving at B without revisting A? Give brief reasons for your answer.
Solution:
Consider the following cube in the 3D space.
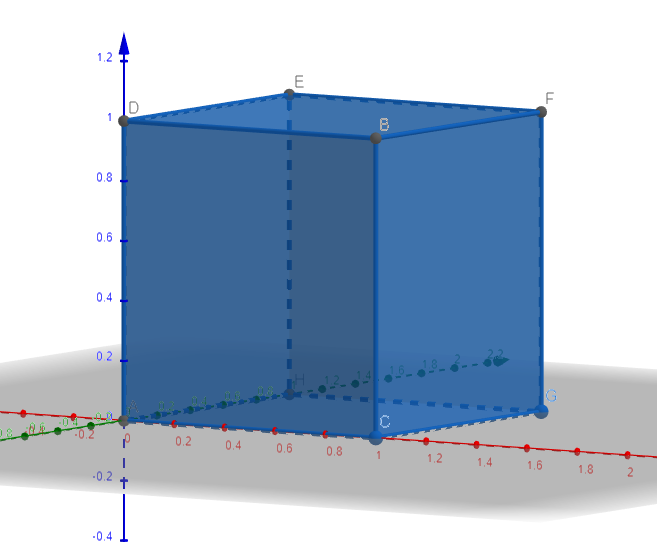
The coordinates of the edges are A(0,0,0), B(1,1,0), C(1,0,0), D(0,1,0), E(0,1,1), F(1,1,1), G(1,0,1).
Let's make some quick observations. First of all, in order to get from (0,0,0) to (1,1,0), one must make an even number of steps on the \(O_z\) and an odd number of steps on \(O_x\) and \(O_y\), where a 'step' means going from one vertex to another one via the rod linking the vertexes. Thus, the total number of steps is even. The number of steps minus 1 is the number of vertexes the ant passes through. Thus, any route leading to B (a route is a collection of steps) involves an odd number of vertexes.
a) The two shortest paths are obviously A-C-B and A-D-B, each having length 2.
b) Since the ant doesn't visit each vertex more than once and the number of vertexes is 8, then it means that the maximum number of vertexes in a route is 7, because the number of vertexes must be odd. We know that the number of steps on \(O_z\) is even, so we have three cases: if the number of steps on \(O_z\) is 0, if the number of steps on \(O_z\) is 2 and if the number of steps on \(O_z\) is 4. However, there is no route with 4 steps on the \(O_z\) axis. If there was such a route, then all the 8 vertexes would be involved, because the ant can only visit each vertex once. Thus, the number of vertexes in the route would be bigger than 7, contradiction.
If the number of steps on the \(O_z\) axis is 0, then we have the routes described in a)
If the number of steps on the \(O_z\) axis is 2, then we can find the route A-H-E-D-B to be possible. This route has length 4, so 4 is a possible length. We can find the route A-H-E-F-G-C-B of length 6, too, so 6 is also a possible length. The route A-H-E-F-G-C-B passes through 7 vertexes, so 6 is the maximum length of a route.
Thus, the possible lengths are 2, 4 and 6.
c) There are 8 paths of length 6: \(A-H-E-F-G-C-B\), \(A-H-G-F-E-D-B\), \(A-C-G-F-E-D-B\), \(A-C-H-H-E-D-B\), \(A-C-G-H-E-F-B\), \(A-D-E-F-G-C-B\), \(A-D-E-H-G-F-B\), \(A-D-E-H-G-C-B\).
d) If the ant travels through each vertex other than A and B twice, then it means that it passes through 14 vertexes, which contradicts the fact that a route from A to B passes through an odd number of vertexes. Thus, such a journey is impossible.
The solution offered by the people making the MAT was similar to what I did. While solving this problem, I remembered of a problem from Thomas Povey's excellent 'Professor Povey's Perplexing Problems', which regarded the number of ways in which an ant can get from an edge of the cube to the opposing edge in a certain number of ways. I was a bit surprised to see a problem using 3D geometry in the MAT, but then I remembered that the A-level core curriculum was a lot more different in 2001 than it is now. Before that, things were even more awkward. I even encountered introductory elements of group theory in a STEP 1 from the 80's. Those times were a lot more...interesting...
Cris.
No comments:
Post a Comment