Let ABC be a triangle with AD as a bisector and AM as a median, with D and M laying on the line BC. Let P be a random point on AD, and E and F the projections of P on the lines AB and AC. If K is the intersection between EF and AM, prove that PK is perpendicular on BC.
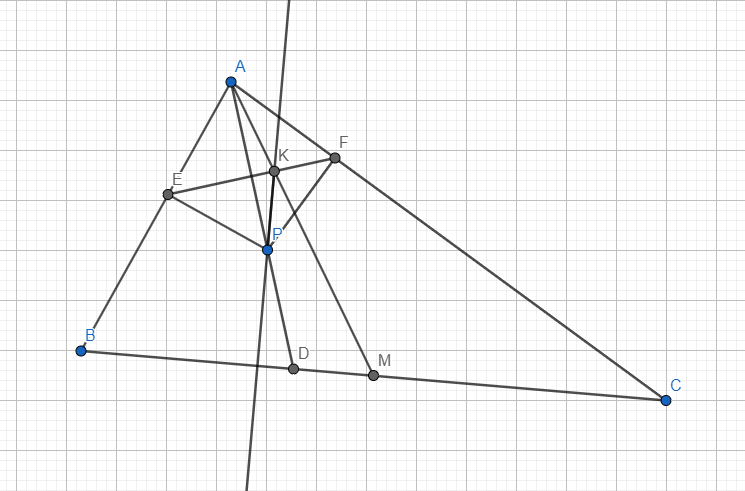
First of all, we shall presume that ABC is not isosceles with AB=AC. If ABC is isosceles with AB=AC, then AD and AM coincide, and PK is obviously perpendicular on DC.
Let us use the transversal theorem in the triangle ABC. We shall consider the transversal E-K-F, and the line denoted by A-K-M, which passes through K. Thus, we get that $$BM \frac{FC}{FA} + MC \frac{EB}{EA} = BC \frac{KM}{KA}$$However, \(AM=MC=\frac{BC}{2}\), so we get that $$\frac{FC}{FA}+\frac{EB}{EA}=2\frac{KM}{KA}$$We shall call this relation (1). By using the property of points on the bisector, we get that \(PE=PF\), and, by triangle congruences, \(AE=AF\). Thus, (1) transforms into \( \frac{FC+EB}{2EA}=\frac{KM}{KA}\). However, \(FC=AC-AF\), and \(EB=AB-AE\), so the relation transforms further into \( \frac{AB+AC}{2EA} -1=\frac{KM}{KA}=r\).
Let us center the complex plane in A. By using the usual notations and by considering AB as the real positive axis, we have that \(e,b⋲R_{+}^*\). We can write \(k=\frac{m+r*a}{1+r}=\frac{m}{1+r}=\frac{b+c}{2(1+r)}\) (2)
Since \( PE⟘AB, PF⟘AC, PE=PF\), it follows that \(\frac{e-p}{b}⋲iR, \frac{f-p}{c}⋲iR, |e-p|=|f-p|\). $$\frac{e-p}{b}⋲iR ⟺ \frac{e-p}{b}=\frac{p^{*}-e^{*}}{b^{*}},$$where \(x^{*}\) is the conjugate of \(x\). $$⟹eb^{*}+e^{*}b=pb^{*}+p^{*}b$$
Similarly, we get that $$fc^{*}+f^{*}c=pc^{*}+p^{*}c$$We shall call these relations (3) and (4) respectively. Apologies for not being able to write the relations next to the equations, I still have to work on my Mathjax skills. I will (probably) learn how to fix this problem in the (far) future. If \(w=cosA+isinA ⟹ f=ew\). \(PK⟘BC ⟺\frac{k-p}{c-b}=\frac{p^{*}-k^{*}}{c^{*}-b^{*}}\).
$$⟺kc^{*}-pc^{*}-kb^{*}+pb^{*}=p^{*}c-ck^{*}-p^{*}b+bk^{*}$$
$$⟺kc^{*}+k^{*}c-bk^{*}-b^{*}k=p^{*}c+c^{*}p-p^{*}b-pb^{*}$$
$$⟺kc^{*}+k^{*}c-k^{*}b-kb^{*}=fc^{*}+f^{*}c-eb^{*}-e^{*}b$$The last line is obtained from combining (3) and (4), and we shall call it (5). Let us replace k as we obtained it in (2). Let us also remember that e and b are positive numbers, so they are equal to their conjugate and modulus.
$$⟹ (5) ⟺ \frac{(b+c)c^{*}}{2(1+r)}+\frac{(b^{*}+c^{*})c}{2(1+r)}-$$
$$-\frac{(b^{*}+c^{*})b}{2(1+r)}-\frac{(b+c)b^{*}}{2(1+r)}=ewc^{*}+ew^{*}c-eb^{*}-e^{*}b$$
$$⟺\frac{|c|^2-|b|^2|}{1+r}=ewc^{*}+ew^{*}c-eb-e^{*}b,$$which shall be known from now on as (6). Let us remember that \(\frac{AB+AC}{2EA}=1+r ⟹\frac{|b|+|c|}{2|e|}=1+r.\)
$$⟹ (6) ⟺ \frac{2e(|c|-|b|)(|c|+|b|)}{|b|+|c|}=ewc^{*}+ew^{*}c-eb-e^{*}b$$
$$⟺ 2(|c|-|b|)=cw^{*}+w^{*}c-2b$$
This shall be known as (7). However, \(c=\frac{w|c|b}{|b|}\).
$$⟹(7)⟺2(|c|-|b|)=ww^{*}b^{*}\frac{|c|}{|b|}+ww^{*}b\frac{|c|}{|b|}-2b$$
$$⟺2(|c|-|b|)=2b\frac{|c|-|b|}{|b|} ⟺ 2=2$$
The last line is true, because |c| is different than |b|, as AB is different than AC. Thus, \(PK⟘BC\) 𞺑
Writing that square at the end of this proof feels so satisfying. The calculations were very tedious when I first solved the problem, but I enjoyed it nonetheless. Of course, in the actual context of Mathematics, this proof isn't hard, but it's a nice exercise for anyone with basic knowledge of complex numbers and with a bit of imagination regarding Geometry.
P.S: This will be the last template update for a while, as I pretty much like this layout of the blog.
Cris.
No comments:
Post a Comment