Solar System's Escape Velocity

This is a step-up from the previous post about the Earth's escape velocity, though this one won't be as exact as the one before. The Solar System is a lot more complicated than what I am about to do, but it's a pretty nice challenge for anyone interested in problems regarding gravity. We shall consider the problem as it was asked by Thomas Povey in his 'Professor Povey's Perplexing Problems' book: only the Sun and Earth affect the escape velocity. Let us calculate the escape velocity from the Solar System, in the reference frame of the Earth's surface. Let \(\alpha\) be the angle at which a probe is sent outside of the Solar System.

First off, a few conventions: the distance between the Sun and the Earth is 149.6 million kilometers, the radius of the sun is 695,508 kilometers, the mass of the sun is \(2*10^{30}\) kilograms, the mass of the Earth is \(6*10^{24}\) kilograms, and the radius of the Earth is 6,371 kilograms, and the gravitational constant G is \(6.6*10^{-11} \frac {N m^2}{kg^2}\).

Let's take a look at the following drawing:



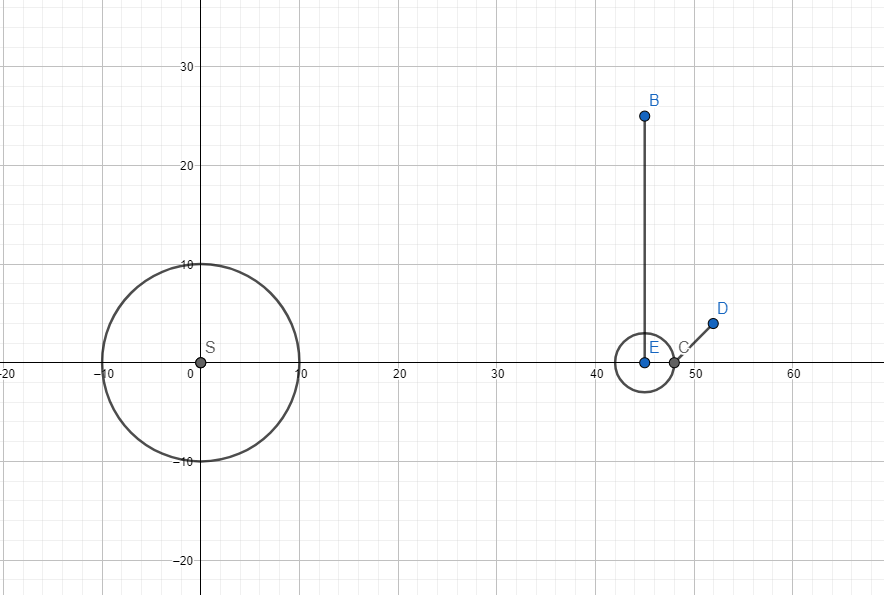
Let S be the center of the Sun, E the center of the Earth. Let the vector CD be the direction our probe is sent outside the Solar System. In order to find the required speed, we first need to find the speed at which the Earth rotates around its own axis, and the speed at which the Earth rotates around the Sun.

$$V_E=W_E R_E$$, where \(W_E\) is the angular velocity of the Earth around its own axis. We know the frequency at which the Earth rotates, the inverse of the number of seconds in a day, \(\frac {1}{86400}\) seconds. Thus, \(W_E = \frac {2\pi}{86400} rad*s^{-1}\). Through an easy calculation, we get that \(V_E=0.47 \frac {km}{s}\).

Now for the speed around the Sun. The frequency of a rotation is \(\frac {1}{86400*365}=\frac {1}{31536000}\). The speed at which the Earth rotates around the sun is \(V_{ES}=W_{ES}R_{ES}\), which is approximately \(30 \frac {m}{s}\).

The next part of the question is to figure out the work required to leave the Solar System. This work is equal to the sum of the work required to escape the Earth and the work required to escape the Sun. Thus, this work is $$W=\int_{R_E}^{\infty} \frac {G M_E m}{r^2} dr + \int_{R_{ES}}^{\infty} \frac {G M_{ES} m}{r^2} dr = \frac {GM_E m}{R_E} + \frac {GM_S m}{R_{ES}}$$. This work must be equal to the kinetic energy, so $$ \frac {GM_E m}{R_E} + \frac {GM_S m}{R_{ES}} = \frac {mv^2}{2}$$

Thus, $$v=\sqrt{2G(\frac {M_E}{R_E} + \frac{M_{S}}{R_{ES}})}=43.67 \frac {m}{s}$$.

Let \(v_i = V_{ES}+V_E = 30.47 \frac {km}{s}\). This is the modulus of the vector \(\vec{CD}\). The escape velocity is the modulus of the difference between the vectors \(\vec{EB}\) and \(\vec{CD}\), where the modulus of EB is \(v\). Let us decompose \(\vec{v_i}\) on the \(O_x\) and \(O_y\) axis. \(\vec{v_i} = v_i cos(\alpha) \vec{i} + v_i sin(\alpha) \vec{j}\). Thus, the required speed is $$v_{esc}=|\vec{v}-\vec{v_i}|=\sqrt {(v - v_i cos(\alpha))^2 + (-v_i sin(\alpha))^2}=$$
$$=\sqrt { v^2-2v*v_i sin (\alpha) +(v_i)^2}$$.

As a small observation, the smallest escape speed is when \(\alpha = \frac {\pi}{2}\), which is equal to roughly 13.2 kilometers per second, while the largest escape speed is when \(\alpha=- \frac{\pi}{2}\), and is roughly equal to 74.2 kilometers per second. The direction is highly important when launching satellites, as can be seen by the given calculations.

It would be fun to find the escape velocity of the Galaxy as the generalization. I did a quick research, and, apparently, the escape velocity of the Galaxy is 537 kilometers per second. That's about 2,073,600 kilometers per hour. For comparison, the fastest man-made object ever is the spacecraft Helios 2, which, in 1989, was moving away from the Earth at a speed of 356,040 kilometers per hour. It's going to take a long while before we leave the Galaxy.

Cris.