Isomorphic groups of integer matrices
My dudes, buckle up, because we're exploring the wonderful realm of abstract algebra again. I found the following problem in the latest number of the 'Gazeta Matematica' by a teacher called Dan Moldovan. I've got to say, the problem is amazing, and I thank this professor for proposing it.
Let \(m,n,p>2\) be natural numbers and let \(G=[A_1, A_2, ... A_p]\) matrices in \(M_{n}(Z)\). To every matrix in G, we attach the reduced matrix modulo m, \(\hat A_i\), so that, if \(A_i=(a_{i,j})\) is out matrix, then the reduced matrix is \(\hat A_i≡(\hat a_{i,j}\), where \(\hat a_{i,j}=a_{i,j}\)(modulo m). Prove that \(\hat G=[\hat A_1, \hat A_2,...\hat A_p]\), together with multiplication in \(M_n(Z)\), forms a group that's isomorphic with G.
Solution:
First of all, let us observe that the neutral element of G isn't \(I_n\). I know this sounds counter-intuitive, but take the group formed by an idempotent matrix with multiplication. The neutral element there is the matrix itself, so any idempotent matrix can be the neutral element of this group. For the sake of the problem, we shall consider the neutral element of G as \(I\). \(I\) has the property that \(I^2=I\), and \(AI=IA=A\) for any element \(A\) in G.
Let us consider the case in which \(I=O_n\). In this case, \(AO_n=A=O_n\), so G={\(O_n\)}, and \(\hat G=[\hat O_n]\), so the two groups are isomorphic.
If \(I\) is different from \(O_n\), then we shall prove that \(gcd(I)=1\). Let \(x=gcd(I)\), and it follows that \(I=xB\), where B is another matrix in \(M_n(Z)\). Since \(I^2=I\), \(x^2B^2=xB\), so \(xB^2=B\). Since \(B^2\) is different than 0 (because otherwise \(I=O_n\)), x divides all elements in B, so \(x^2\) divides all elements of I, which implies that \(x=1\).
I found the following lemma in the excellent article 'Finite Groups of Matrices Whose Entries Are Integers', published in AMC in 2002 by Mr. James Kuzmanovich and Mr. Andrey Pavlichenkov.(https://www.jstor.org/stable/2695329)
Lemma: Let G be a group of integer matrices in which there is an element \(A\) such that \(A^q=I\), with q prime, and \(\hat A=\hat I\), where \(\hat A\) is the reduced matrix modulo p, where p is another prime number. It follows that \(A=I\).
Proof: Since \(\hat A=\hat I\), \(A=I+pH_1\). Let \(gcd(H_1)=d\)
⟹\(A=I+pdH\), where \(gcd(H)=1\).
⟹\(A^q=(I+pdH)^q=I+\sum_{k=1}^q {{q}\choose{k}}(pd)^{k}H^k I^{q-k}=I\). However, \(I^n=I\), for all n, so \(\sum_{k=1}^q {{q}\choose {k}}(pd)^{k-1}H^k I=O_n\) (I divided by \(pd\). The only element without \(p\) in it is is \(qHI\), so p divides q, and, thus, p is q or p is 1. Since p is prime, p is q, and, by dividing the relation once more, we get that p divides \(gcdH\), so p is 1, which is a contradiction. Thus, \(H=O_n\), so \(A=I\).
Back to our problem, I shall prove something that probably everyone saw coming: the fact that \(f(X)=\hat X\) is the isomorphism we were looking for, where \(\hat A\) is the reduced matrix modulo m. Obviously, \(\hat I\) is the neutral element in \(\hat G\), and all the calculations are the same, so f is a morphism. Since \(G\) and \(\hat G\) are finite, we have to prove that the morphism is injective. For that, we shall prove that \(Ker (f)=[I]\).
Let us presume by absurd that there is an A in G such that \(f(A)=\hat A=\hat I\). Thus, \(A=I+mB\), so, because G has order p, \((I+mB)^p\). Let q be a prime factor of p. Thus, we have that
$$⟹((I+mB)^\frac{p}{q})^q=I$$
Since \(\frac {p}{q}=k\) is an integer, \((I+mB)^k=I+mH_1\), so \((I+mH_1)^q=I\).
$$⟹\sum_{j=1}^q {{q}\choose{k}}(mH_1)^j I=O_n$$
Let \(gcd H_1=d\), so \(H_1=dH\), with \(gcd(H)=1\). Thus,
$$\sum_{j=1}^q (md)^{j-1}H^j I= \sum_{j=1}^q (md)^{j-1} H^j =O_n$$
By using the same logic as before, \(md | qH\). Since \(gcd(H)=1\), m divides q, and, since m is bigger than 1, m is q. Because both m and q are prime, we can use the lemma, and, thus, H=0, so \((I+mB)^k=I\).
By applying this algorithm to all the prime divisors of k, we end up with \(mB=O_n\), so \(B=O_n\), so \(A=I\). Thus, Ker(f)={I}, so the morphism f is injective, and, consequently, bijective, so \(G\) and \(\hat G\) are isomorphic. This concludes the proof.
I can't really think of a paragraph ending this article, which is a total shame, since this problem was magnificent. I have an excuse though: I have the MAT in a few days, and I am a bit stressed out. I think I'll go play some World of Warcraft to relax. After the MAT, I will try posting more problems, though I came to realize the problems I post while under pressure are longer and harder than the normal problems I post. Maybe it's some kind of psychological mechanism behind this... I'm not foreshadowing the psychology article, btw.
Cris.
Functional Equation Involving Integrals
I'm working on a very interesting problem which I will post these days. In the meantime, here's a nice functional equation that I solved yesterday. This problem, in a changed form, was shortlisted for the 2015 Romanian NMO (National Maths Olympiad). The problem goes as follows:
Find all the functions \(f:[0,1]➝ℝ\) such that \(\int_0^x f(t)dt = f(x)^n+f(x)\), for a fixed odd n.
Solution:
Let us consider the function \(z(x)=x^n+x\).
\(\frac{dz}{dx}=x^{n-1}+1>0\), so z is strictly increasing. It is obvious that the function is surjective, so \(z\) is bijective, and, thus, it has an inverse. Returning to the equation at hand, $$z(x)^{-1}∘(\int_0^x f(t)dt)=f(x)$$and, since the integral and z are differentiable, f is also differentiable, and, thus, continuous.
Now that we know that \(f\) is differentiable, we can differentiate the equation with respect to \(x\), obtaining that
$$f(x)=nf(x)^{n-1}f '(x)+ \text{f '(x) (I)} $$
Let us look now at the set \(A=[x|f([0,x])=0]\). By putting \(x=0\) in the equation, we can deduce that \(f(0)=0\), so A is not void. \(A\) is also compact, so it has a supremum, M. By the inertia theorem, there is an interval \([M,x_0]\) such that the function keeps constant sign on that interval, with \(x_0\) being the smallest possible number with this property. If \(x_0=1\), then we have no problem. If \(x_0<1\), then it means that \(f(x_0)=0\). However, by looking at equation \((I)\), we can deduce that, if \(f(x)>0\), then \(f '(x)>0\); if \(f(x)=0\), then \(f '(x)=0\); if \(f(x)<0\), then \(f '(x)<0\). Since the sign of the function is constant on \([M,x_0]\), the function is increasing on \([M,x_0]\), and, thus, it is 0 on the interval, so \(x_0\) would be the supremum of A, which contradicts the way we chose M. This implies that the function keeps constant sign after M, and, thus, is either increasing or decreasing after M.
From now on, we shall focus on proving that \(M=1\). For the simplicity of calculations, we shall write \(f(x)=y\). If \(y>0\), then \(y'>0\). We can rearrange (I) into the form
$$1=ny^{n-2}y'+ \frac{y'}{y}$$
and, by integrating, we get that
$$\frac{n}{n-1}y^{n-1}+ln(y)-x+k=0$$
However, due to the continuity of the function, $$\lim_{x\to M}\frac{n}{n-1}f(x)^{n-1}+ln(f(x))-x+k=-∞<0$$which is a contradiction. Thus, \(f\) isn't bigger than 0, and, similarly, \(f\) isn't smaller than 0, which means that \(f(x)=0, ∀x∊[0,1]\).
The problem was quite intuitive if you think about it. It seemed pretty obvious that \(f\) can't be different than 0, but that's how most hard analysis problems are: you are asked to prove something that is intuitively correct, but incredibly hard to formalize. This exercise wasn't particularly hard, but I found it pretty instructive and rather fun. Tune in next time for an article about some isomorphism on groups of integers matrices (if I manage to learn enough Latex to make the hats (^) above classes modulo p).
Cris.
Ant on a Cube
A set of 12 rods, each 1 metre long, is arranged so that the rods form the edges of a cube. Two corners, A and B, are picked with AB the diagonal of a face of the cube. An ant starts at A and walks along the rods from one corner to the next, never changing direction while on any rod. The ant’s goal is to reach corner B. A path is any route taken by the ant in travelling from A to B.
(a) What is the length of the shortest path, and how many such shortest paths are there?
(b) What are the possible lengths of paths, starting at A and finishing at B, for which the ant does not visit any vertex more than once (including A and B)?
(c) How many different possible paths of greatest length are there in (b)?
(d) Can the ant travel from A to B by passing through every vertex exactly twice before arriving at B without revisting A? Give brief reasons for your answer.
Solution:
Consider the following cube in the 3D space.
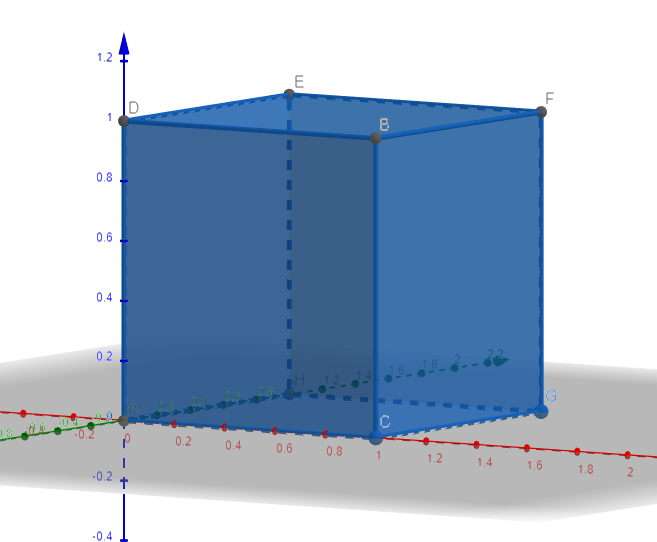
The coordinates of the edges are A(0,0,0), B(1,1,0), C(1,0,0), D(0,1,0), E(0,1,1), F(1,1,1), G(1,0,1).
Let's make some quick observations. First of all, in order to get from (0,0,0) to (1,1,0), one must make an even number of steps on the \(O_z\) and an odd number of steps on \(O_x\) and \(O_y\), where a 'step' means going from one vertex to another one via the rod linking the vertexes. Thus, the total number of steps is even. The number of steps minus 1 is the number of vertexes the ant passes through. Thus, any route leading to B (a route is a collection of steps) involves an odd number of vertexes.
a) The two shortest paths are obviously A-C-B and A-D-B, each having length 2.
b) Since the ant doesn't visit each vertex more than once and the number of vertexes is 8, then it means that the maximum number of vertexes in a route is 7, because the number of vertexes must be odd. We know that the number of steps on \(O_z\) is even, so we have three cases: if the number of steps on \(O_z\) is 0, if the number of steps on \(O_z\) is 2 and if the number of steps on \(O_z\) is 4. However, there is no route with 4 steps on the \(O_z\) axis. If there was such a route, then all the 8 vertexes would be involved, because the ant can only visit each vertex once. Thus, the number of vertexes in the route would be bigger than 7, contradiction.
If the number of steps on the \(O_z\) axis is 0, then we have the routes described in a)
If the number of steps on the \(O_z\) axis is 2, then we can find the route A-H-E-D-B to be possible. This route has length 4, so 4 is a possible length. We can find the route A-H-E-F-G-C-B of length 6, too, so 6 is also a possible length. The route A-H-E-F-G-C-B passes through 7 vertexes, so 6 is the maximum length of a route.
Thus, the possible lengths are 2, 4 and 6.
c) There are 8 paths of length 6: \(A-H-E-F-G-C-B\), \(A-H-G-F-E-D-B\), \(A-C-G-F-E-D-B\), \(A-C-H-H-E-D-B\), \(A-C-G-H-E-F-B\), \(A-D-E-F-G-C-B\), \(A-D-E-H-G-F-B\), \(A-D-E-H-G-C-B\).
d) If the ant travels through each vertex other than A and B twice, then it means that it passes through 14 vertexes, which contradicts the fact that a route from A to B passes through an odd number of vertexes. Thus, such a journey is impossible.
The solution offered by the people making the MAT was similar to what I did. While solving this problem, I remembered of a problem from Thomas Povey's excellent 'Professor Povey's Perplexing Problems', which regarded the number of ways in which an ant can get from an edge of the cube to the opposing edge in a certain number of ways. I was a bit surprised to see a problem using 3D geometry in the MAT, but then I remembered that the A-level core curriculum was a lot more different in 2001 than it is now. Before that, things were even more awkward. I even encountered introductory elements of group theory in a STEP 1 from the 80's. Those times were a lot more...interesting...
Cris.
Interesting property of intersecting normal subgroups
I didn't think I'd talk about this either up until a few minutes ago.
The Romanian Maths Curriculum is extremely intriguing, mainly because of the fact that we do Analysis (at least Olympiad students do) and Linear and Abstract Algebra during our high school years. From what I've gathered, in College, we go again through these subjects in the first year, but at a more advanced level. The students who attended the Maths Olympiad during high school have a one year head-start over the ones that didn't, if you think about it, and that doesn't apply only for the Romanian Olympians who go to Universities in Romania. Participating at the Olympiad helps greatly in College, as the Olympians have more time to socialize and focus on extra-curricular activities during the first year, because they already know a lot of what the teacher is showing during the first few months. There is, however, a downside; only a few other people will have time to socialize with the Olympians, because in most Universities, there aren't a lot of people who already know a big chuck of the Curriculum.
I stumbled upon this group theory problem today, while going through a popular abstract algebra book. The problem itself, I think, is rather well known, but I discovered something that surprised me about the groups that the problem discusses.
Let \((G,*)\) be a group of order 2n, and \((H,*)\) and \((K,*)\) normal subgroups of order n such that \(H∩K={e}\). Prove that G is abelian.
Solution:
I shall prove that the only group satisfying these conditions is G={e, a, b, ab}, with \(a^2=b^2=e\), and a and b commute.
Since H and K have order n, and their intersection is e, their reunion has 2n-1 elements. Let x be the element that isn't in \(H∪K\). As a fun fact, since x isn't in \(H∪K\), \(x^{-1}\) isn't in \(H∪K\) either, because then x would be in either H or K, contradiction. Thus, \(x=x^{-1}\), so \(x^2=e\). This, however, doesn't really impact our proof. For the rest of the proof, we shall consider H* and K* as H and K minus {e}.
Let \(f_x:H^*⟶K^*\), \(f_x(h)=xh\). Obviously, this function is injective, and, since \(H^*\) and \(K^*\) have the same cardinal, it's bijective. Also, the function is well-defined, because \(xh\) can't be in H, because, if \(xh_1=h_2\), then \(x=h_2*(h_1)^{-1}\), so x would be in H.
Since the function is bijective, we have that \(xh_i=k_i\), for any i between 1 and n-1. Thus, \(x=k_i*(h_i)^{-1}=k_j*(h_j)^{-1}\), for any i and j between 1 and n-1, so \((h_i)^{-1}h_j=(k_i)^{-1}k_j\). The RHS belongs to H, and the LHS belongs to K, and we know that the only element of the intersection between H and K is e, so \(h_i=h_j=h, k_i=k_j=k\) for any i and j. Thus, H={e,h} and K={e,k}, while G is isomorphic with Klein's group: {e, h, k, hk}, and, as a fun fact, G is abelian, as required. The solution that the author of the book offered relied mostly on the fact that x has order 2, and that H and K were normal groups. The problem, as stated in the book, didn't say that H and K were normal subgroups, but rather asked you to prove that in the first part of the problem.
I've got to say, this result is a pretty intriguing property of Klein's group if you think about it. I truly hope that I didn't get anything wrong in the proof. Of course, this result pales in front of theorems such as the classification of simple finite groups, which took thousands of pages to write. However, it is a modest start. Tune in next time, for either another Analytical Geometry problem, another Probability problem, that personality article I kept talking about, or something totally random (again).
Cris.
An Old Problem from the Balkan Maths Olympiad
It was either this, or yet ANOTHER probability post. I thought of spicing things up a bit.
Here in Romania, coordinate geometry is described vaguely at the end of the 10th grade. I haven't seen exercises that involve thought in our curriculum regarding this subject, and, as an enthusiast of geometry, this saddened me, because analytic geometry is one of the stepping stones into University Mathematics. I managed to find coordinate geometry problems in MATs and STEPs, and, after a while, I managed to find one in the most prestigious Balkan competition: The Balkan Mathematical Olympiad. The problem I am about to solve is the 4th problem from the 1986 BMO. Like most other geometry problems, it has a synthetic solution, one which I will not discuss in this article. Frankly speaking, I like analytic solutions more than synthetic ones, because it gives me the rightful impression of manipulating real life objects (geometric figures) through numbers. The problem goes something like this:
The circles \(K_1\) and \(K_2\), centered at \(O_1\) and \(O_2\), with radii 1 and \(\sqrt 2\), respectively, intersect at A an B. Let C be a point on \(K_2\) such that the midpoint of AC lies on \(K_1\). Find the length of the segment AC if \(O_1 O_2 =2\).
Solution:
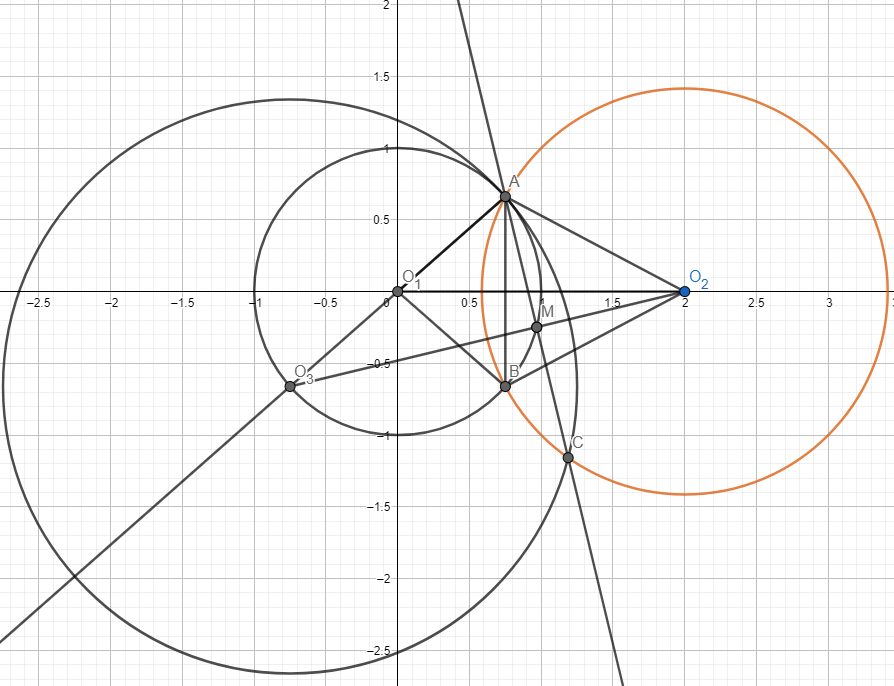
Let us consider \(O_1\) as the origin of the Cartesian plane, and \(O_2 (2,0)\), \(A(x_a, y_a)\), \(B(x_b, y_b)\), \(C(x_c, y_c)\).
We shall look at the triangle \(AO_1O_2\). By the cosine theorem, we have that $$(AO_1)^2+(O_1 O_2)^2-2O_1O_2 * AO_1* cos(\angle AO_1O_2) = (AO_2)^2$$Thus, \(cos (\angle AO_1O_2)=\frac{3}{4}\), and, consequently, \(sin (\angle AO_1O_2)=\frac{\sqrt 7}{4}\). We now know that \(x_a=\frac{3}{4}, y_a=\frac{\sqrt 7}{4}\). Now that we know exactly where A is, we can take a closer look at C. Let M be the midpoint of AC. Since M is on \(K_1\), and \(x_m=\frac{x_a+x_c}{2}\), \(y_m=\frac{y_a+y_c}{2}\), we can use the equation of the circle to see that \(\frac{x_{c}^2}{4}+\frac{9}{16}+\frac {3x_c}{8}+\frac{7}{64}+\frac{y_{c}^2}{4}+\frac{\sqrt {7} x_c}{8}=1\), and, thus, \(x_{c}^2+\frac{3}{2}x_c+y_{c}^2+\frac{\sqrt 7}{2}y_c=3\). By adding 1, we have that C lies on the circle with equation \((x_c+\frac{3}{4})^2+(y_c+\frac{\sqrt 7}{4})=4\) This circle has center \(O_3 (-\frac{3}{4}, -\frac{\sqrt 7}{4})\), which is the diametrically opposite point of A in regards to the circle centered in \(O_1\). It is easy to observe that A is on the circle centered in \(O_3\) with radius 2, too, so AM is the height of the triangle \(AO_{3}O_{2}\). It is easy to find the cosine of \(\angle AO_2O_3\) through the cosine theorem. $$(O_{2}C)^2+(O_2O_3)^2-2O_2O_3cos(\angle AO_2O_3)=(O_3C)^2$$and, thus, the required cosine is \(\frac{3}{4}\). Consequently, we can find \(sin(\angle AO_2O_3)=\frac {\sqrt 7}{4}\). We shall now calculate the area of \(AO_2O_3\) in two different ways. We know that $$S_{AO_3O_2}=\frac{AM*O_3O_2}{2}=\frac{AO_2*O_2O_3*sin(\angle AO_2O_3)}{2}$$
$$⟹AM=\frac{\sqrt 14}{4} ⟹ AC=\frac{\sqrt 14}{2}$$.
It was pretty surprising to find such a problem in an international Maths competition. As I said, analytic geometry isn't really discussed in the Romanian curriculum, and, from what I've seen, isn't really part of the curriculum of contests either. The thing with analytic geometry is that, at an advanced level, it's a bridge between analysis, topology and other fields of Mathematics. The importance of Geometry is obvious by looking at the Millennium Prize Problems: the Poincare conjecture. While it's proof doesn't involve Geometry per-se, its implication is partly geometrical. I have a lot of ideas for the next article, but I think that I will either write an article about Jungian psychology (new tag boys!), or I will solve a very interesting probability problem that I found in the Step 2 from last year. Or, and this one is most likely, I will decide the subject on the spot.
Cris.
Here in Romania, coordinate geometry is described vaguely at the end of the 10th grade. I haven't seen exercises that involve thought in our curriculum regarding this subject, and, as an enthusiast of geometry, this saddened me, because analytic geometry is one of the stepping stones into University Mathematics. I managed to find coordinate geometry problems in MATs and STEPs, and, after a while, I managed to find one in the most prestigious Balkan competition: The Balkan Mathematical Olympiad. The problem I am about to solve is the 4th problem from the 1986 BMO. Like most other geometry problems, it has a synthetic solution, one which I will not discuss in this article. Frankly speaking, I like analytic solutions more than synthetic ones, because it gives me the rightful impression of manipulating real life objects (geometric figures) through numbers. The problem goes something like this:
The circles \(K_1\) and \(K_2\), centered at \(O_1\) and \(O_2\), with radii 1 and \(\sqrt 2\), respectively, intersect at A an B. Let C be a point on \(K_2\) such that the midpoint of AC lies on \(K_1\). Find the length of the segment AC if \(O_1 O_2 =2\).
Solution:

Let us consider \(O_1\) as the origin of the Cartesian plane, and \(O_2 (2,0)\), \(A(x_a, y_a)\), \(B(x_b, y_b)\), \(C(x_c, y_c)\).
We shall look at the triangle \(AO_1O_2\). By the cosine theorem, we have that $$(AO_1)^2+(O_1 O_2)^2-2O_1O_2 * AO_1* cos(\angle AO_1O_2) = (AO_2)^2$$Thus, \(cos (\angle AO_1O_2)=\frac{3}{4}\), and, consequently, \(sin (\angle AO_1O_2)=\frac{\sqrt 7}{4}\). We now know that \(x_a=\frac{3}{4}, y_a=\frac{\sqrt 7}{4}\). Now that we know exactly where A is, we can take a closer look at C. Let M be the midpoint of AC. Since M is on \(K_1\), and \(x_m=\frac{x_a+x_c}{2}\), \(y_m=\frac{y_a+y_c}{2}\), we can use the equation of the circle to see that \(\frac{x_{c}^2}{4}+\frac{9}{16}+\frac {3x_c}{8}+\frac{7}{64}+\frac{y_{c}^2}{4}+\frac{\sqrt {7} x_c}{8}=1\), and, thus, \(x_{c}^2+\frac{3}{2}x_c+y_{c}^2+\frac{\sqrt 7}{2}y_c=3\). By adding 1, we have that C lies on the circle with equation \((x_c+\frac{3}{4})^2+(y_c+\frac{\sqrt 7}{4})=4\) This circle has center \(O_3 (-\frac{3}{4}, -\frac{\sqrt 7}{4})\), which is the diametrically opposite point of A in regards to the circle centered in \(O_1\). It is easy to observe that A is on the circle centered in \(O_3\) with radius 2, too, so AM is the height of the triangle \(AO_{3}O_{2}\). It is easy to find the cosine of \(\angle AO_2O_3\) through the cosine theorem. $$(O_{2}C)^2+(O_2O_3)^2-2O_2O_3cos(\angle AO_2O_3)=(O_3C)^2$$and, thus, the required cosine is \(\frac{3}{4}\). Consequently, we can find \(sin(\angle AO_2O_3)=\frac {\sqrt 7}{4}\). We shall now calculate the area of \(AO_2O_3\) in two different ways. We know that $$S_{AO_3O_2}=\frac{AM*O_3O_2}{2}=\frac{AO_2*O_2O_3*sin(\angle AO_2O_3)}{2}$$
$$⟹AM=\frac{\sqrt 14}{4} ⟹ AC=\frac{\sqrt 14}{2}$$.
It was pretty surprising to find such a problem in an international Maths competition. As I said, analytic geometry isn't really discussed in the Romanian curriculum, and, from what I've seen, isn't really part of the curriculum of contests either. The thing with analytic geometry is that, at an advanced level, it's a bridge between analysis, topology and other fields of Mathematics. The importance of Geometry is obvious by looking at the Millennium Prize Problems: the Poincare conjecture. While it's proof doesn't involve Geometry per-se, its implication is partly geometrical. I have a lot of ideas for the next article, but I think that I will either write an article about Jungian psychology (new tag boys!), or I will solve a very interesting probability problem that I found in the Step 2 from last year. Or, and this one is most likely, I will decide the subject on the spot.
Cris.
The Probability of Passing a Test
Have you ever attended a test without studying anything whatsoever before it? Well your boy Cris is here to tell you something: you most certainly failed. Or, at least, you would have most certainly failed in a world fully governed by A-level Mathematics. I managed to find last year's STEP today, and I decided to take a look at some of the problems. Apart from the tedious, VERY TEDIOUS calculations, I found a nice problem that many people will emphasize with. This problem was the last Probability exercise in Step 1 last year.
A multiple-choice test consists of five questions. For each question, n answers are given
(n > 2) only one of which is correct and candidates either attempt the question by choosing
one of the n given answers or do not attempt it.
For each question attempted, candidates receive two marks for the correct answer and lose
one mark for an incorrect answer. No marks are gained or lost for questions that are not
attempted. The pass mark is five.
Candidates A, B and C don’t understand any of the questions so, for any question which
they attempt, they each choose one of the n given answers at random, independently of their
choices for any other question.
(i) Candidate A chooses in advance to attempt exactly k of the five questions, where
k = 0, 1, 2, 3, 4 or 5. Show that, in order to have the greatest probability of passing
the test, she should choose k = 4 .
(ii) Candidate B chooses at random the number of questions he will attempt, the six
possibilities being equally likely. Given that Candidate B passed the test find, in
terms of n, the probability that he attempted exactly four questions.
(iii) For each of the five questions Candidate C decides whether to attempt the question
by tossing a biased coin. The coin has a probability of \(\frac{n}{n+1}\) of showing a head, and
she attempts the question if it shows a head. Find the probability, in terms of n, that
Candidate C passes the test.
Solution:
(i) The probability of getting a correct answer to a question is \(\frac{1}{n}\). If k is smaller than 3, then the passing score isn't achieved in any scenario, so the probability of passing for k<3 is 0.
If k=3, then the probability is \(\frac{1}{n^3}\).
If k=4, then the probability of passing is \({4}\choose{3}\)\(\frac{n-1}{n^4}+\frac{1}{n^4}=\frac{4n-3}{n^4}\).
If k=5, then the probability of passing is \( {5}\choose{4}\)\(\frac{n-1}{n^5}+\frac{1}{n^5}\). In the last case, the minimum number of possible correct answers is 4, because otherwise the passing mark isn't achieved. Let us now compare the probabilities we found.
$$\frac{4n-3}{n^4}>\frac{1}{n^3}⟺4n-3>n⟺n>1$$.
$$\frac{4n-3}{n^4}>\frac{5n-4}{n^4}⟺4n^2-3n>5n-4⟺4(n-1)^2>0$$
Thus, the biggest probability of passing is when k=4.
(ii) We shall use Bayes' theorem for this one. Bayes' theorem states that, if we want to calculate the probability that the even B happens given that another event A happened before, then the probability required is \(P(B|A)=\frac{P(B⋂A)}{P(A)}\). Thus, the probability of B passing is $$P(k=4|pass)=\frac{P((k=4)⋂pass)}{P(pass)}=$$
$$=\frac {\frac{4n-3}{n^4}}{\frac{5n^2+2n-4}{n^5}}=$$
$$=\frac{4n^2-3n}{5n^2+2n-4}$$
(iii) \(P(C|pass)=\frac{10n^3}{(n+1)^5}*\frac{1}{n^3}+\frac{5n^4}{(n+1)^5}*\frac{4n-3}{n^4}+\frac{n^5*(5n-4)}{n^{5}*(n+1)^{5}}=\frac{25n-9}{(n+1)^5}\).
The problem itself was rather easy, and the calculations were simple enough to be done quick enough. The Step this year had some really interesting geometry problems, and, from what I've heard, had a monster algebra problem. While I find Step questions insanely interesting, I find the calculations required a bit tedious.
I attended a contest similar to the one described in the problem when I was younger. I am pretty sure many kids across the world, too, participated at the Mathematical Kangaroo competition. It was a rather good mental exercise for kids, in which you were asked to solve 30 questions in an hour and a half or something. I never did good in multiple choice tests, so I didn't have insanely good results at it; if I recall correctly, I once started crying desperately in one such contest, and the teacher assisting us was afraid to take my paper when the time concluded. Yikes!
Cris.
Subscribe to:
Comments (Atom)

