Here in Romania, coordinate geometry is described vaguely at the end of the 10th grade. I haven't seen exercises that involve thought in our curriculum regarding this subject, and, as an enthusiast of geometry, this saddened me, because analytic geometry is one of the stepping stones into University Mathematics. I managed to find coordinate geometry problems in MATs and STEPs, and, after a while, I managed to find one in the most prestigious Balkan competition: The Balkan Mathematical Olympiad. The problem I am about to solve is the 4th problem from the 1986 BMO. Like most other geometry problems, it has a synthetic solution, one which I will not discuss in this article. Frankly speaking, I like analytic solutions more than synthetic ones, because it gives me the rightful impression of manipulating real life objects (geometric figures) through numbers. The problem goes something like this:
The circles \(K_1\) and \(K_2\), centered at \(O_1\) and \(O_2\), with radii 1 and \(\sqrt 2\), respectively, intersect at A an B. Let C be a point on \(K_2\) such that the midpoint of AC lies on \(K_1\). Find the length of the segment AC if \(O_1 O_2 =2\).
Solution:
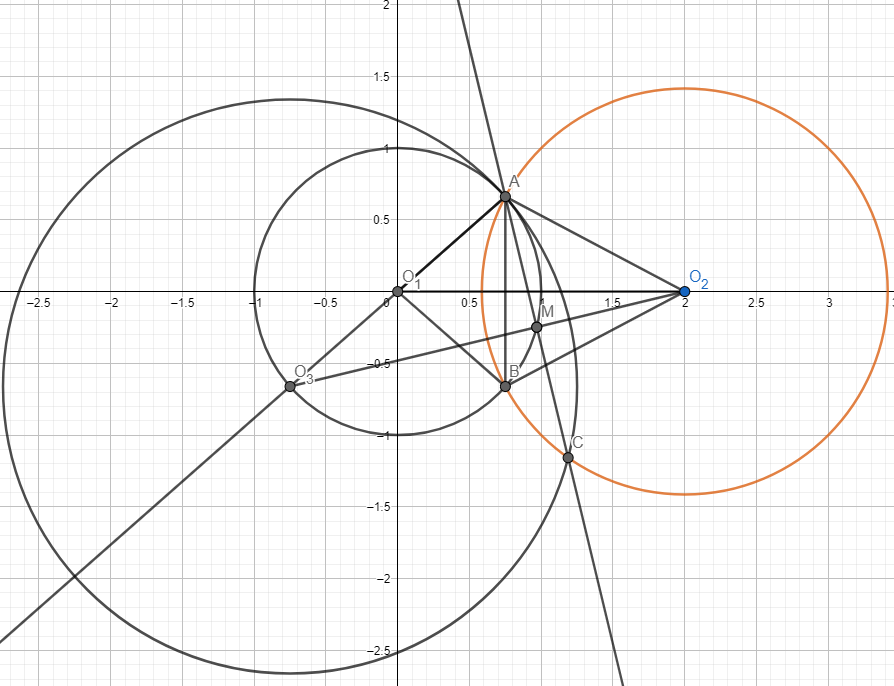
Let us consider \(O_1\) as the origin of the Cartesian plane, and \(O_2 (2,0)\), \(A(x_a, y_a)\), \(B(x_b, y_b)\), \(C(x_c, y_c)\).
We shall look at the triangle \(AO_1O_2\). By the cosine theorem, we have that $$(AO_1)^2+(O_1 O_2)^2-2O_1O_2 * AO_1* cos(\angle AO_1O_2) = (AO_2)^2$$Thus, \(cos (\angle AO_1O_2)=\frac{3}{4}\), and, consequently, \(sin (\angle AO_1O_2)=\frac{\sqrt 7}{4}\). We now know that \(x_a=\frac{3}{4}, y_a=\frac{\sqrt 7}{4}\). Now that we know exactly where A is, we can take a closer look at C. Let M be the midpoint of AC. Since M is on \(K_1\), and \(x_m=\frac{x_a+x_c}{2}\), \(y_m=\frac{y_a+y_c}{2}\), we can use the equation of the circle to see that \(\frac{x_{c}^2}{4}+\frac{9}{16}+\frac {3x_c}{8}+\frac{7}{64}+\frac{y_{c}^2}{4}+\frac{\sqrt {7} x_c}{8}=1\), and, thus, \(x_{c}^2+\frac{3}{2}x_c+y_{c}^2+\frac{\sqrt 7}{2}y_c=3\). By adding 1, we have that C lies on the circle with equation \((x_c+\frac{3}{4})^2+(y_c+\frac{\sqrt 7}{4})=4\) This circle has center \(O_3 (-\frac{3}{4}, -\frac{\sqrt 7}{4})\), which is the diametrically opposite point of A in regards to the circle centered in \(O_1\). It is easy to observe that A is on the circle centered in \(O_3\) with radius 2, too, so AM is the height of the triangle \(AO_{3}O_{2}\). It is easy to find the cosine of \(\angle AO_2O_3\) through the cosine theorem. $$(O_{2}C)^2+(O_2O_3)^2-2O_2O_3cos(\angle AO_2O_3)=(O_3C)^2$$and, thus, the required cosine is \(\frac{3}{4}\). Consequently, we can find \(sin(\angle AO_2O_3)=\frac {\sqrt 7}{4}\). We shall now calculate the area of \(AO_2O_3\) in two different ways. We know that $$S_{AO_3O_2}=\frac{AM*O_3O_2}{2}=\frac{AO_2*O_2O_3*sin(\angle AO_2O_3)}{2}$$
$$⟹AM=\frac{\sqrt 14}{4} ⟹ AC=\frac{\sqrt 14}{2}$$.
It was pretty surprising to find such a problem in an international Maths competition. As I said, analytic geometry isn't really discussed in the Romanian curriculum, and, from what I've seen, isn't really part of the curriculum of contests either. The thing with analytic geometry is that, at an advanced level, it's a bridge between analysis, topology and other fields of Mathematics. The importance of Geometry is obvious by looking at the Millennium Prize Problems: the Poincare conjecture. While it's proof doesn't involve Geometry per-se, its implication is partly geometrical. I have a lot of ideas for the next article, but I think that I will either write an article about Jungian psychology (new tag boys!), or I will solve a very interesting probability problem that I found in the Step 2 from last year. Or, and this one is most likely, I will decide the subject on the spot.
Cris.
nais
ReplyDelete