Two Analysis problems of completely different flavours

Eyy guys, it's your boy Cris here, writing this post during the first day of uni here at Imperial College. Hooray! Today, I shall discuss two problems that I have found or thought about while being here.

The first problem of the day is a limit asked at a contest. This problem was given to me at a party organized by the halls I live in. While the party continued in the background, for about 15 minutes, my universe consisted of me and the limit. I guess that's what happens when you ask STEM people to have fun. The limit is more of an icebreaker for the harder pure Analysis thingy that follows. The limit goes something like this:

Find the limit of \((\frac{a_1^{1/n}+a_2^{1/n}+a_3^{1/n}}{3})^n\) as n approaches infinity, where \(a_1, a_2, a_3\) are real positive numbers.

Solution:

I'm not really a fan of calculating limits or integrals, I'm more of an Algebra person, but here it goes. Write the fraction as \((\frac{a_1^{1/n}+a_2^{1/n}+a_3^{1/n}}{3})^n=(1+\frac{a_1^{1/n}+a_2^{1/n}+a_3^{1/n}-3}{3})^n\). Then, we shall use the exponential limits. Thus, after a bit of calculations, we end up finding that the limit of the initial sequence is the limit of \(e^{\frac{n}{3}(a_1^{1/n}+a_2^{1/n}+a_3^{1/n}-3)}\). Thus, what is left for us to do is calculate the upper limit. However, it is easy to prove that, as \(x\) tends towards 0, the limit of \(\frac{a^x-1}{x}\) is \(ln(a)\), using L'Hospital's rule. Thus, after applying this to our limit, we get that the limit is \((a_1*a_2*a_3)^{\frac{1}{3}}\). Of course, we can generalize the problem by adding m variables instead of 3, and we would get the geometric mean of all the m variables.

The problem appeared on a multi-choice contest, as far as I've been told. The guy who told me the problem gave me the result, and asked me to prove it. I think I solved it in about 20 minutes, after a few failed attempts at trying some inequalities. I'm certain that someone more passionate about Calculus could have solved it way quicker than I did, but the limit was fun to think about nonetheless.

The next problem, and the actual purpose of this article, is a problem about rotating bodies that appeared on this year's Traian Lalescu contest, at the B section; the section for Engineering departments. It caused some troubles among students, as it used a trick that is not that well known. Here it goes:

Let \(f:[a,\infty]→[0,\infty]\) a monotone and continuous function, such that \(\int_{a}^{\infty} f(x) dx\) is convergent. The graph of the function, alongside the coordinate axes, contain a surface of area A.
1. Prove that, for all natural numbers n, there exist the points \(x_1, x_2,...x_n∊[a,\infty]\) such that the lines \(x=x_k\) split the domain in n parts of equal area.
2. Let \(a_n=\frac{\sum_{k=1}^{n} f(x_k)}{n}\) Prove that V, the volume obtained by rotating the curve determined by f around the \(OX\) axis, is finite, and that \(\lim_{n\to\infty} a_n=\frac{V}{πA}\).

Solution:

Part 1 is fairly straightforward to prove, so it is left as an exercise to the reader (mainly because I am too lazy to write it down lmao). The second part is what the problem is all about.

The volume of the rotated solid is \(V=π*\int_{a}^{\infty}f^2(x) dx\), so we want to prove that the limit is equal to \(\frac{\int_{a}^{\infty} f^2(x) dx}{\int_{a}^{\infty} f(x) dx}\).

Now, here comes a dank meme. Kids, don't let your parents try this at home.Now, here comes a dank meme. Kids, don't let your parents try this at home.

Let \(F(x)\) be the integral from a to x of the function. Thus, \(F(x_k)=\frac{k}{n}A\). Also, F is clearly bijective, so we can write \(x_k=F^{-1}(\frac{k}{n}A)\), so \(f(x_k)=f(F^{-1}(\frac{k}{n}A)\). Thus, after a few calculations, we can write \(a_n=A^{-1}\frac{\sum A*f(F^{-1}(\frac{kA}{n})}{n}\). As n tends towards infinity, the sum becomes an integral, so the limit of \(a_n\) will become \(A^{-1}\int_{0}^{A}f(F^{-1}(x))dx\).

We shall prove that \(\int_{0}{A}f(F^{-1}(x))dx=\int_{a}^{\infty}f^2(x)dx\). In order to do this, we apply the change of variable \(t=F^{-1}(x)\), and, after calculations, get the required result.

The big trick with this problem is that it required that \(F^{-1}\) part. That is a well-known trick in Romania, as a problem similar to this one was asked in 2009 at the Olympiad (I think it was in 2009). A similar problem was also asked at the entrance exam for a programme at the Ecole Polytechnique in France. As always, the problem was pretty fun to solve, yet it required a trick fit for the Olympiads. 

Before ending the article, I want to make an announcement: I'm finally launching a theory page! I wish to share my knowledge of stuff among students who wish to partake at College competitions such as the IMC. The first theory page will be for Linear Algebra and it will cover everything from basic vector spaces to the Jordan decomposition. I will update that theory page from time to time, whenever I can; don't expect updates to be constant though, since it is pretty tough to cope with courses, out of class learning (I'm studying Complex Analysis atm; expect the next problem to be about Complex Analysis) and social life all at once. I will, however, do my best. So, as always, tune in next time, for something completely random!

Cris.

Results in Number Theory proved with different integral domains

What's up people? As you can see, this isn't an applied maths post, as I promised before. I still have such a post in mind; basically, my idea is to create a system of differential equations that models all sorts of relationships based on the Sociotype. The idea is there, and so are the mathematical methods, I just need a bit of field work. But asking random people on the street to take an obscure test on the internet alongside their partners and then trying to quantify their enthusiasm and level of involvement in the relationship is a bit too much, so I'll probably end up posting the solution of the Gompertz equation or the prey-predator model.

But, until then, I decided I'd take a look at a subject I didn't really care about throughout high school: number theory. I devoted most of my time to algebra, and a bit of it to analysis, but, after seeing the beauty of these results, I really regret it. I'm probably gonna study some algebraic number theory in my free time to compensate for my lack of knowledge.

So there I was, in Bulgaria, surfing AoPS, when I saw some Number Theory problem, with a guy commenting that it's similar to Lagrange's 4 squares theorem. I checked it out on Wikipedia (great place for that, right?), and, apparently, it is solvable with quaternions, numbers of the form \(x=a+ib+jc+kd\), with \(i^2=j^2=k^2=ijk=-1\), and \(ij=k, jk=i, ki=j, ji=-k, kj=-i, ik=-j\).

The theorem states that any natural number can be written as a sum of 4 squares. More intuitively, it states that, if you have a sphere in 4 dimensions, then that sphere contains an integer point on its contour. In order to prove this, we shall use a sub-field of the quaternions, the Hurwitz quaternions, which are numbers of the form \(x=a+ib+jc+kd\), with \(a,b,c,d\) all integers or halves of odd numbers.

First, let us note that, if two numbers can be written as the sum of 4 squares, then their product can be written in that form, too. Indeed, presume that \(x=a^2+b^2+c^2+d^2, y=e^2+f^2+g^2+h^2\). The sum of 4 squares is the modulus of a quaternion with integer coefficients, and, thus, \(xy\) would be the modulus of the product of quaternions with integer coefficients, which, in turn, is the modulus of a quaternion with integer coefficients. This concludes the fact that \(xy\) can be written as a sum of 4 squares.

With this fact, we can resume to proving that every prime can be written as a sum of 4 squares. We know that any odd prime divides a number of the form \(1+l^2+m^2\). We shall now discuss the Hurwitz primes, which act literally like the normal prime numbers, but belong to the quaternions. They are literally prime quaternions.

Let us presume that a prime odd number \(p\) is a Hurwitz prime. Then, \(p|1+l^2+m^2=(1+li+mj)(1-li-mj)\), so \(p\) divides either \(1+li+mj\) or \(1-li-mj\). However, this means that \(p\) divides each coefficient, so it divides 1 too, which is false. Thus, no odd prime is a Hurwitz prime.

Since \(p\) isn't a Hurwitz prime, we can write it as the product of two different Hurwitz quaternions, so \(p=(a+bi+cj+dk)(e+fi+gj+hk)\). By taking modulus, we get that \((a^2+b^2+c^2+d^2)*(e^2+f^2+g^2+h^2)=p^2\), so both of them are equal to \(p\), because, otherwise, their product wouldn't be an integer. If at least one of the sums is composed only of integers, then everything is great. Otherwise, we shall denote \(x=\frac{+/- 1 +/- i +/-j +/- k}{2}\), such that \(p+x\) has only even coefficients. Let \(y=p+x\). Then, \(p=(y^*x-1)(yx^*-1)\), where \(a^*\) is the conjugate of \(a\), while the products belong to the Hurwitz quaternions with integer coefficients, called Lipschitz quaternions. This concludes the proof.

After this, I thought that maybe I could extend the thought processes of this proof to prove easier results. I wanted to prove that any prime number that is a multiple of 4 plus 1 can be written as the sum of two squares. We know that, for such a prime number \(p\), \(-1\) is a quadratic residue, so there is an \(m\) such that \(p|1+m^2\).

I want to prove that \(p\) isn't a Gaussian prime. If \(p\) were a Gaussian prime, then \(p|1+m^2=(i+m)(m-i)\) implies that \(p\) divides both \(m\) and 1, which is a contradiction. Thus, \(p\) isn't a Gaussian prime, so \(p=(a+ib)(c+id)\), with \(a,b,c,d\) integers. By taking the modulus again, we get that both sums are equal to \(p\), which concludes the proof. As a fun fact, any number of the form \(4k+1\) can be written as a product of conjugate Gaussian primes.

Just reading this article makes me wanna study some Number Theory. In Romania, Number Theory isn't treated too much in schools, and, except for the students that participate at TSTs, everyone else stops learning this subject in the 6th grade. Somehow, though, this makes a bit of sense: Number Theory and Algebra go hand in hand in a majestic way, as I just proved, and any interesting proof in this subject would require some Ring Theory. Anyway, I'm gonna go now. Tune in next time for some Ring Theory, Applied Maths, or something completely random!

Cris.

The creativity of youth - my thoughts on a sub-genre of science fiction

What's up, diggity dogs? (that's from Mung from 'Chowder'). I had many plans for this post, ranging from IMO problem 1, solving the Gompertz equation, solving some problems from the IMC, proving a result in Thermodynamics, you name it. However, ever since my national exam, the Romanian 'Bacalaureat' exam, I developed an interest in Literature. You see, my parents encouraged me to read when I was younger, but, being the stubborn guy that I am, I decided I wouldn't read. I can only do things that I come up with. After studying Literature intensively for some time before the exam, I found out that it's not that bad, and I started reading more. This morning, I bought a sci-fi book written by a Romanian sci-fi writer, and now that I finished it, I came up with the idea to talk a bit about what is called 'mundane science fiction', and why it might appeal to people.

First of all, let's make a distinction between 'soft' sci-fi and 'hard' sci-fi. The hard science fiction focuses on scientific accuracy. While, of course, things aren't entirely accurate (because if they were, the book would be considered a doctorate thesis, not a work of fiction), the science introduced is made somewhat plausible. In soft sci-fi, all bets are off. Soft science fiction also might concern itself with more societal problems, such as George Orwell's '1984', Turtledove's 'In the presence of mine enemies' and so forth. Basically, soft sci-fi encompasses everything from 'Star Trek', 'Star Wars' and the 'Warhammer 40K' universe to alternate history, while hard sci-fi talks about more plausible advances, such as Isaac Asimov's work, or, in movies, 'Project Almanac', perhaps even 'Donnie Darko', or 'Stranger Things'. I'm still meditating over the MCU, yet it might be somewhere in the middle, leaning towards soft sci-fi (I know how to find eigenvalues too, yet I don't know how to time travel, speaking of 'Endgame').

'Mundane sci-fi' (which is quite an ugly term for a nice genre if you ask me) is a sub-genre of hard sci-fi which deals with 'down to Earth' situations. Literally. Fast travel between planets, stars, whatever is not invented in these worlds, with the situations being as realistic as possible, while still containing lots of fiction. I'd say that the most well known book belonging to this genre is Carl Sagan's 'Contact'. I'm not hesitant to admit, but what really got me in this genre was the anime 'Steins; Gate'. I'd call this genre 'realistic sci-fi' rather than 'mundane sci-fi'. The book I read was 'The Ribbon of Time', by George Lazar, in which a group of students discover a means of predicting the future. The lecture was really great, especially since it included lots of technical hardware details that actually made sense. As I said, I liked it so much, that I finished it in a few hours. I myself have been juggling with writing a book belonging to this genre since 2016-2017, I even posted a bit of it on Wattpad (here it is if you want to check it out: https://www.wattpad.com/446606017-red-horizon-foreword). My attraction to this genre made me try to analyse it literally.

Like most modern works of literature, the accent falls on defining the characters. From what I've observed, character dialogue dominates the book, with narration falling on the second place. The narration is mostly used to introduce character interaction and inventions, though this isn't necessarily the norm. The dialogue not only makes the story seem more dynamic, but it also makes the reading more dynamic. It won't make the reading faster, but it will make the reader lose track of time. In this aspect, modern books are made for people who live more hurried lives, who can read only in their rare free time. While classical books are still necessary, they are no longer fit for the society: ordinary readers don't have time to understand slow paced action, which revolves mostly around artistic methods that are hard to follow. Among the characters of the mundane sci-fi genre are necessarily STEM educated academics, and the main characters may be STEM educated, too. Either way, the plot revolves around a scientific discovery that is somehow meant to change the world. The narrative usually follows a pre-determined path: a group of people discovers something, which leads to perfecting, testing and studying the discovery, which eventually leads to a climax point in which the characters use their invention in a way that may involve global actions. The ending is, usually, thought provoking, and, due to the lecture's proximity to the real world, the message is contemporary with the modern world. This genre also permits intersection with all other sorts of modern genres, such as horror, comedy, romance, etc.

As I promised earlier, I'd try to psychologically analyze how this genre works. Remember my post about cognitive functions in Jungian typology? Well, let's apply them here. I'd postulate that this genre attracts anyone with Ti and Ne as the two most powerful functions in the function stack. Ne would desire creative ideas and an escape from a boring world (or perhaps the world is only boring for me, who knows), while the more rationally inclined Ti would want scientific accuracy. In this case, this sci-fi genre is the best for ENTPs and INTPs that are more scientifically inclined. I'd assume that dominant Si users would be interested in this type of genre, too, due to its realism. Ni users would be more interested in the far future rather than a fiction based on the present, while the lack of suspense and physical action in the genre wouldn't interest the Se user. Over all, I think that this realistic sci-fi mostly attracts ENTPs (like me), INTPs, ISTJs and ISFJs. It is quite curious how the types attracted by this genre are somewhat opposite. That is not to say that other types can't be attracted to the genre: indeed, I believe that most STEM focused individual might be somewhat intrigued by the idea of this genre. However, I believe that the types I mentioned would be definite fans. During the 21st century, when people's lives are becoming more and more streamlined, I'd expect most of the audience to turn to a sci-fi or fantasy setting while reading. I also believe that, somehow, these genres might also reflect ideas from childhood, dreams of a paradise where everything is possible. The fantasy world of youth changes from games to books, and, by studying this kind of literature, readers might be able to live a more interesting life and even re-live dreams of childhood adventures.

Well, I guess that was all for today. Apologies for any grammatical errors: my laptop is broken, and I sent it to a service, so I'm writing this from my tablet. The keyboard of the tablet is rather small, so I might have miss-clicked a few letters. Tune in next time for probably an Applied Mathematics/Physics post, or something completely random!

Cris.

Basic properties of Markov Matrices

What's up people? A few minutes ago, while I was browsing AoPS, I saw a post about Markov matrices. Being the curious guy that I am, I immediately jumped on Wikipedia to see what they are all about. Apparently, a Markov matrix, also known as a Stochastic matrix (you've got to admit though, Markov matrix sounds a little bit more complex) is a matrix used in probability and statistics in order to find out how a system develops. A Markov matrix usually encodes a Markov chain (this guy surely has many things named after him). Initially, Andrej Markov wanted to use these matrices for linguistic analysis and card shuffling, yet they ended up being used in many other fields. In this article, I want to discuss several interesting properties of these matrices. 

First of all, let me define a Markov matrix. A matrix \(A=(a_{i,j})_{0<i,j<n+1}\) with positive elements is a right stochastic matrix if the sum of the elements on each row is 1, and A is a left stochastic matrix if the sum of the elements on each column is 1. A first, rather obvious property, would be the following:

1. If \(A∈M_n(R)\) is a right stochastic matrix, then \(A^T\) is a left stochastic matrix.

The proof of this property is rather simple and straightforward.

Since the Markov matrix represents how a system goes from one state to another in the Markov chain, the product of two stochastic matrices is also a stochastic matrices.

2. If \(A, B\) are right/left stochastic matrices, then \(AB\) is also a right/left stochastic matrix.

We shall prove that the sum of the elements on the first row is 1. One can observe that the other rows have the same property. 

Let \(C=AB\). Thus, \(c_{11}=a_{11}b_{11}+a_{12}b_{21}+...+a_{1n}b_{n1}\), and, in the end, after summing all the elements and taking the common factor, we'll get exactly what we wanted, that the sum of the elements on the row is 1.

Now, we shall get to the eigenvalues of a Markov matrix.

3. Let \(A\) be a right stochastic matrix. Then all its eigenvalues have absolute value smaller or equal to 1.

Let us consider an eigenvector \(v\) and let \(v_i\) be its greatest element in absolute value. We know that \(Av=av\), where \(a\) is an eigenvalue of \(A\). By finding the value of the product on the i-th column, we get that \(a_{i1}v_1+...+a_{in}v_n=av_i\). We shall write this as a module, and, thus, \(|a_{i1}v_1+...+a_{in}v_n|=a|v_i|≤a_{i1}|v_1|+...+a_{in}|v_n|≤|v_i|\), so \(|a|≤1\), as required.

In fact, I believe that a stronger result can be established.

4. Let \(A\) be both a right and a left stochastic matrix. If \(a\) is an eigenvalue for which there is an eigenvector with the property that the sum of its elements is different than 0. Then, \(a=1\).

Yet again, we look at \(Av=av\). For every row, we have that (a_{i1}v_1+...+a_{in}v_n=av_i\). We sum up these relations for each row, and we get that \(v_1+v_2+...+v_n=a(v_1+v_2+...+v_n)\), because the sum on columns is equal to 1. Since the sum of the elements of the eigenvector is different from 0, we can just divide by it and obtain that \(a=1\).

This property is really interesting, because it tells us that the Markov matrices have one known eigenvalue, if such an eigenvector exists. In fact...

5. 1 is always an eigenvalue of a Markov matrix.

In order to prove this, let us first observe that, if \(A\) is a left stochastic matrix, then \(A^T\) is a right stochastic matrix. By hand, we can check that \([1 1 ... 1]^T\) is an eigenvector of \(A^T\) with eigenvalue 1. Since \(A\) and \(A^T\) have the same eigenvalues, we conclude that \(A\) has eigenvalue 1.

The property that \(A\) and \(A^T\) have the same eigenvalues is well known, yet I believe that a short explanation is in order. Take the characteristic polynomial of \(A\), \(p(X)\). We know that \(p(A)=O\), and, by transposing, \(p(A^T)=O\). Thus, we know that not only does \(A^T\) have the same eigenvalues as \(A\), but the eigenvalues also have the same multiplicities.

This was but an introduction in  the study of Markov matrices. I believe that the properties I described are good enough for a first impression on this topic. I don't know too much probability (you may have seen that I only tackled the STEP 2 probability problems, because I don't know advanced probability), but when I find out more, I'll be sure to discover more properties of these matrices. Tune in next time for probably something regarding the IMO or the IMC (since the IMC starts this week), or something completely random!

Cris.

Matrix problem regarding rational points and a number theory lemma

Eyy there. I was gonna write an article about Markov matrices (which is almost complete, btw), but then, while scrolling through undergrad contests, I found a really neat solution for a problem at the CIIM from last year. The CIIM is a competition for Latin American undergrad students, similar to IMC, Putnam, Seemous and Traian Lalescu. From what I've seen, the problems are a bit harder than those at IMC, but, then again, my opinion isn't necessarily a very competent one. These are the problems (great for you if you know Spanish).



Today, we shall solve the first one (because you know I like matrices). For those that don't know Spanish, here's what it says:

Problem: Prove that there exists a \(2*2\) matrix of order 6 with rational entries, such that the sum of its entries is 2018.

Solution: Let \(A\) be a matrix with the required properties. Since \(A^6=I_2\), we get that \((A-I_2)(A+I_2)(A^2+A+I_2)(A^2-A+I_2)=O_2\). The minimal polynomial of \(A\) is, thus, one of those appearing in the decomposition, since \(A\) is rational. If \(A+I_2=O_2\), then the order of \(A\) is 2. If \(A-I_2=O_2\), then the order of \(A\) is 1. If \(A^2+A+I_2=O_2\), then \(A^3=I_2\). Thus, the only possibility is that \(A^2-A+I_2=O_2\), so \(Tr(A)=1\), \(det(A)=1\). Let \(a, b, c, d\) be the elements of \(A\), in that order. Thus, we know that \(a+d=1\), and \(ad-bc=1\). By writing \(d=1-a\), we get that \(a(1-a)-bc=1\), so \(a-a^2-bc=1\). We want to prove that there exist matrices with these properties such that \(a+b+c+d=2018\), which is equivalent to \(c=2017-b\). Thus, our end goal is proving that \(a-a^2-2017b+b^2=1\) has rational solutions.

Now, we shall write this as the equation of a hyperbola. \(\frac{1}{4}+a-a^2-2017b+b^2+2017^2=\frac{5}{4}+2017^2\), and, by multiplying by 4, we get that \((2b-4034)^2-(2a-1)^2=5+4*2017^2\). However, we know that any odd number can be written as a difference of squares (\(2k+1=(k+1)^2-k^2\), so there exist two real squares for which we get that conclusion. In fact, we can even calculate \(a\) and \(b\), but that is left as an exercise for the reader. Since we found that \(a\) and \(b\) exist, and we found all the rational entries of the matrix according to the rational numbers \(a\) and \(b\), we conclude that there is indeed a matrix with the required properties.

As a fun fact, initially, I made a calculation mistake. Instead of writing the equation as a hyperbola, I wrote it as the equation of a circle. Thus, I got that \((2b-4034)^2+(2a-1)^2=5+4*2017^2\). I do not know whether the above equation has rational solutions, but, while trying to solve it, I remembered of an old problem from Gazeta Matematica 11/2017, proposed by Marian Andronache, which shall be treated as a lemma:

Lemma: Let \(n\) be a natural number bigger than 1 with the sum of its divisors not divisible by 4. Prove that \(n\) can be written as the sum of two squares.

Proof: We shall use the well-known 'sum of two squares theorem', which states that a number can be written as a sum of two squares if and only if any prime divisor of the form \(4k+3\) appears in the decomposition at an even power. I won't get into details regarding the solution to this, but you can see a proof of this theorem here: https://www.math.uchicago.edu/~may/VIGRE/VIGRE2008/REUPapers/Bhaskar.pdf

Getting back to the lemma, let us presume by absurd that \(n\) can't be written as a sum of two squares. Thus, there is an odd number of apparitions of a prime number\(p_i\) of the form \(4m+3\). We know that the sum the divisors is \(S(n)=\prod_{k=1}^{w(n)} \frac{p_k^{a_k+1}-1}{p_k-1}\), where \(a_k+1\) is the power at which a prime number appears in the decomposition. The term from the product associated with \(p_i\) is equal to \(1+p_i+p_i^2+...+p_i^{a_i}\), and, because \(a_i\) is odd, we get that the sum is a multiple of 4, which contradicts our choice of \(n\). The sum is a multiple of 4, because \(p^{2k}\) is a multiple of 4 plus 1, while \(p^{2k+1}\) is a multiple of 4 plus 3, and we can group the terms together.

I was a bit sad to find out that the above lemma doesn't work on the problem. Indeed, the sum of all divisors of \(5+4*2017^2\) is a multiple of 4. It does, however, work on, for example, \(1+4*2017^2\). I was just 4 units away. The lemma that I wrote has some interesting applications, and I might search for some problems to solve using it for the next articles. Thinking about that, I haven't posted any number theory problem so far. I might post something after I'm done with the Markov matrices article. Tune in next time for some properties of stochastic matrices, or something completely random!

Cris.

Two Linear Algebra problems of completely different flavours

Eyy, what's up - what's down? I have my final high school exams this week, and, after that, I'll be free to study anything I want. I already started looking into tensor products and metric spaces (I know, kinda unrelated), and I really hope I can upgrade the level of Maths on this blog by the end of summer. I really wish to learn more advanced Maths topics, so I could also do some neat Physics.

Anyways, before my final exams, I thought that I should post something fun, in case I don't make it lmao. So here are my picks for this article! Of course, they are linear algebra problems, but I promise I will soon change the topic. As much as I'd love linear algebra (it's my favourite part of Mathematics at the moment), this blog is called 'Cris's Science Blog', not 'Cris's Linear Algebra Blog'.

The first problem comes from an Excellence Test from Timisoara. I was searching through some old Mathematical magazines of mine, and I found a remarkable number from the RMT (Revista Matematica Timisoara, the Mathematical Magazine of Timisoara), the one made for the 2017 Maths Olympiad. Of course, it brought back memories, since that was my brightest year. That particular number was dedicated to the memory of one of the greatest Mathematics teachers Romania ever had, Gheorghe Eckstein.

This problem looks like an X and O with matrices. Suppose you have a \(2n * 2n\) matrix, that is 'empty' at first. Two players, A and B, take successive  turns at writing numbers in the matrix. Once a number was written, it can't be erased. A wins if the determinant of the matrix isn't 0, while B wins if the determinant is 0. The question asks if there exists a strategy for which B always wins, no matter what A does.

Solution: After playing with my imaginary friends for a while, I figured out that there is, indeed, a strategy. Since the matrix doesn't involve any known numbers, it was safe to assume that the strategy consisted of doing something with the lines of the matrix.

Consider the first two lines of the matrix. If A puts a number \(x\) on the first line, B should put the same number right under it. By repeating this process, there will be two equal lines. Since the number \(2n\) is even, B will always be the one ending the process, and, thus, he will be in control of the determinant. It doesn't matter what A puts in the other lines; if A puts a number on one of the other lines, B can randomly put a number there, too. Eventually, A will be the one writing a number on one of the first lines, and B will duplicate that number.

The problem wasn't exactly hard, but it was a fun game. That's why I added the 'Intriguing Puzzles' tag.

Now comes a more scientific one. This one is taken from Evan Chen's 'Napkin'. I started studying University Maths from there, and I really recommend checking it out: http://web.evanchen.cc/napkin.html

Let V be a finite dimensional vector space, and let \(T: V->V\) be a linear map, and let \(T^n:V->V\) denote T applied n times. Prove that there exists an integer N such that \(V=Ker(T^N)⊕Im(T^N)\).

Solution: In order to talk about a direct sum, I want to prove that there is an N after which \(Ker(T^N)⋂Im(T^N)=Φ\). It is easy to see that, as N increases, the Kernel of the linear map increases, while the dimension decreases. Since V is finite dimensional, the dimension of the Kernel reaches a maximum, let's call it l. I want to prove that, after it reaches this maximum, the Kernel and the Image become distinct. Since the dimension of the Kernel remains the same, it is obvious that the Kernel will remain the same after iterations. Let N be the iteration of T for which the Kernel remains constant afterwards.

Let \(a\) be in both \(Ker(T^{N+1})\) and \(Im(T^{N+1})\). I want to prove that \(a=0\). We know that \(T^N(a)=O\), and, since a is in the image, we have that \(T^{2N+1}(b)=0\), for b, the pre-image of a. Thus, we know that b is in \(Ker(T^{2N+1})=Ker(T^{N})\). But, since \(T^{N+1}(b)=a\), we get that \(a=0\), exactly as we wanted, so we can talk about a direct sum.

Now, we know that \(dim (Ker(T^N) ⊕ Im(T^N)) = dim Ker(T^N) + dim Im(T^N) = dim V\), and, since the Kernel and the image are subspaces of V, we get that their direct sum is exactly V, as we wanted.

I found this problem rather interesting, and, from what I saw, it works as a lemma. I haven't tried writing this as actual vector spaces instead of abstract notations, but I might look into it. Until then, I have to study Literature for my exam on Monday. Wish me luck, and more posts are coming! At first, they'll still be Linear Algebra, but after a while, trust me, they'll become more diverse. Tune in next time for something completely random about matrices!

Cris.

Equality in Sylvester's Inequality

Alright, back to the monthly posts. I have my final exams at the end of the month, after which I plan on studying more advanced Physics and College Maths. I'm already making progresses, as you may see after this post.

A while ago, one of my good friends showed me the problems he had to solve at the National phase of the Traian Lalescu contest. The first problem seemed rather interesting, and, as the title says, it involves an equality for the Sylvester inequality. As you may know, the Sylvester inequality states that, for two matrices \(A\) and \(B\) in \(M_n(C)\), \(rank(AB)≧ rank(A)+ rank(B)-n\). In this article, I will prove that, for any matrix \(A\) in \(M_n(C)\), \(n≧2\) and for any polynomial \(f\) of degree \(m≧1\) with the free coefficient \(a\) different from 0, we have that \(rank(f(A)*A)=rank(f(A))+rank(A)-n\).

Solution:

We know the fact that the rank of a matrix is the dimension of the image of the morphism associated with the matrix. By the dimension theorem, \((dim(Im (f(A)*A))+dim (Ker (f(A)*A))=n\), so \(dim(Ker (f(A)*A))=n-rank(f(A)*A))\), and, by using the dimension theorem for the other matrices and re-writing the equation in the conclusion, we need to prove that \(dim Ker(f(A)*A))=dim Ker (f(A))+dim Ker (A)\).

We shall now prove that \(Ker (f(A)*A)=KerA⊕Ker(f(A))\). First of all, let's prove that the direct sum between the two vector spaces exists. Let \(Z\) be an element of the Kernel of A different than 0. Thus, \(AZ=O\). Let m be the free coefficient of f. Thus, \(f(A)*Z=m*Z=O\) only if m is 0, which is false. Thus, no element of Ker(A) is in Ker(f(A)) other than the zero vector, so we can talk about a direct sum. We know that \(dim Ker A + dim Ker (f(A)) = dim (Ker A ⊕ Ker (f(A))\). Let us write \(W=Ker A⊕ Ker f(A)\).

We shall get back to proving that \(W=Ker(f(A)*A)\). Let \(Z=xX+yY\) be an element of W. We shall prove that it belongs to \(Ker(f(A)*A)\). \(f(A)*AZ=f(A)*A*(xX+yY)=f(A)*A*xX+A*f(A)*yY=O\), so we have proved that W is included in \(Ker(f(A)*A)\). Conversely, let \(Z\) be an element of \(Ker(f(A)*A)\). \(f(A)*A*Z=O\), so \(AZ\) belongs to Ker(f(A)). \(A*f(A)*Z=O\), so \(f(A)*Z\) belongs to \(Ker(A)\). Since \(AZ\) belongs to Ker(f(A)), \(f(A)*Z-aZ\) belongs to the Kernel, too.  Using the assertion that we've proven earlier, that W is included in \(Ker(f(A)*A)\), we get that \(f(A)Z-f(A)*Z+aZ\) is included in \(Ker(f(A)*A)\), so \(Z\) is included, too, because m is different than 0. Thus, \(Ker(f(A)*A)\) is included in W, and this implies that W is equal to \(Ker(f(A)*A)\). This concludes the proof.

The problem in the contest was a bit different, because the polynomial the jury chose was f(A)=mI-A. The generalized problem that I solved is much more interesting though. I always wondered how to reach the equality in Sylvester's inequality, and this problem sheds some light on that. However, this isn't my biggest curiosity in the realm of linear algebra. Back in the 11th grade, I was so scared of failing at the Olympiad, that I started dreaming problems at night. Here's one that I have no idea how to solve: what is the number of nilpotent matrices of order n with all entries being either 0 or 1? Of course, for n odd, there are no such matrices, but what happens for even n? I asked a friend to make a computer program, so we could compute the number. We did n=2 and n=4, but n=6 would have taken a few days to compute, so we gave up. If you know the solution to the problem I dreamt, make sure to send me a link in the comments! Tune in next time, for something completely random!

Cris.

Two matrix problems from recent Romanian Maths Olympiads

I normally don't do this kind of posts, but this year's ONM (this is the Romanian National Mathematics Olympiad; in Romanian, the adjectives and modifiers are placed after the noun) has been rather... awkward. The problems themselves were beautiful, I can't disagree, yet some were too easy for a National Olympiad, while some were too hard. The median score for the 12th grade was 3 points, and bronze medals were given to those with a score above 3.5, while silver medals were given to those with a score above 5 points. For comparison, at the 11th grade, silver medals were given to those with a score above 20 points.

This post can be regarded as a complaint to the Olympiad Committee. Last year, the subjects at the 11th grade were incredibly hard, while this year, they were incredibly easy. This difference between difficulty makes it harder for students to properly prepare for the Olympiad, and leads to anomalies in the hierarchies: hard subjects imply that students get points based on how much they guess (I put emphasis on the word 'guess') from the official solution, while easy subjects imply that many people solve them. As an example, I will discuss the solutions of the first problem from both Olympiads: the 2018 ONM and the 2019 ONM. I picked these problems because, usually, the first problems are the easiest during the contest. Even at the International Maths Olympiad, the first problem of each day is regarded as the easiest.

Problem one from ONM 2018: For every column vector X in \(M_{n,1}(Z)\), let \(c(X)\) be the least common divisor in the vector. Let A be a nxn matrix with integer entries. Prove that the following affirmations are equivalent:
1) \(|det(A)|\)=1.
2) \(c(AX)=c(X)\), for every vector X.

Solution:
1) implies 2) can be done by a double inequality. Obviously, c(AX) is bigger or equal to c(X), so we get that \(c(X)=c(A*A^{-1}X)≧c(AX)≧c(X)\), so \(c(AX)=c(X)\).
2) implies 1) is a bit harder. The official solution involves something regarding systems of equations, yet I solved it with a theorem regarding integer matrices. Any matrix A with integer entries can be written as A=U*J*V, where U and V are integer matrices with determinant of modulus 1, while J is a diagonal matrix with the integer elements \(d_1, d_2, ...d_n\) on the diagonal, in this order, such that \(d_1 | d_2 |... |d_n\).
By using this property, let us look at \(c(AX)=c(UJVX)\). By choosing \(X=V^{-1}X\), we get that \(c(UJVV^{-1}X)=c(UJX)=c(V^{-1}X)=c(X)\), because of the first implication. We shall now look at \(c(UJX)\) In order to prove that A has determinant plus or minus 1, we have to prove that J has only plus or minus 1 on its diagonal. Also, \(c(UJX)=c(JX)\), because JX is another vector. We shall look at \(c(JX)=c(X)\). Thus, for a vector \(X=(d_n, d_n, ... d_1)\), by doing JX, we get that \(d_1=d_n\). By taking an X such that \(c(X)=1\), we get that \(d_n=1\). Thus, the determinant of J has modulus 1, and A itself has modulus 1. This concludes the problem.

As you can see, the problem had a few intriguing ideas. The theorem made the whole problem easier, but it was still pretty hard. The official solution involved much more creativity. In total, about 5 people managed to solve this problem. I believe that this problem is good for the Olympiad, though it should be more of a problem 4 rather than one of many problems of same difficulty.

Let us get to the present day now...

Problem one from ONM 2019: Let A and B be complex nxn matrices such that there exists an idempotent matrix C with the property that C*=AB-BA. Prove that \((AB-BA)^2=O\).

Solution:
If C is idempotent, that means that its determinant is either 0 or 1. If its determinant is 1, then all its eigenvalues are 1, and, thus, the adjoint matrix has the same eigenvalues. With this in mind, the trace of C would be n, while the trace of AB-BA is 0, which is a contradiction. Thus, the determinant of C is 0. Let us use Sylvester's inequality on this: we have that \(rank(C^{*} C)≧ rank(C) + rank (C^{*}) - n\). With this in mind, \(n≧rank(C)+rank(C^{*})\). If \(rank(C)=n-1\), then rank (C*)=1, which implies that \(C^{*2}=Tr(C^{*})*C=O\) by writing C* in the specific form of a matrix with rank 1. If rank(C) is smaller or equal to n-2, then, by definition, C* is O, so \(AB-BA=O\). In both cases, \((AB-BA)^2=O\)

These properties of the adjoint matrix are well known in the Romanian Olympiad system. The problem is, in essence, hard, but most teachers show their students the properties of the adjoint matrix. I believe that this problem is a good opening problem, though, provided that the test increases in difficulty later on. This problem was solved by 52 students during the contest.

The point I'm really trying to make is that there must be a middle ground. An Olympiad's purpose should be to encourage children in following their passion, yet extremely hard or extremely easy problems might actually discourage them. Both problems become really easy if similar problems have been discussed before during class, yet the difference between them is that the first one involves a theorem that is not normally discussed in high school, while the second one only involves the 11th grade curriculum. A student may be able to solve the second problem even if he's never seen anything like it before, given enough creativity, but it would be impossible for him to re-discover the theorem used in the first problem. The official solution involves much more creativity than should be expected from one of the easier problems in the contest, and only a small fraction of the students, the best of the best, can come up with it. Yet the Olympiad isn't only about the top 5 students, but about all participants. During the 12th grade Olympiad this year, only 6 out of the 59 participants solved at least one problem, while the rest wrote down every idea they had with the hopes of it being in the official solution. Only one student solved more than two problems. I agree, the Olympiad shouldn't be easy, but it shouldn't be borderline impossible either.

This shouldn't be taken as an insult addressed to the Olympiad Committee. It's not. It's simply a complaint and a reason for the complaint. Besides, both problems are very beautiful, they truly represent high school Mathematics. But some problems, even though they are beautiful, just aren't meant for contests.

Alright folks, that's it for today. Tune in next time, for complex numbers, some algebra, or something completely random!

Cris.

Proof of the Riemann Hypothesis using a group with proper subgroups of order 2 and 3

1. Introduction

Back in 1859, German mathematician Bernhard Riemann introduced us to 6 important hypotheses...



Just kidding, did you really think I'd solve the Riemann Hypothesis here? April Fools joke!

Half of the title is correct, though. Today, we shall discuss a problem from the 2016 Maths Olympiad shortlist, proposed by Mihai Piticari. The problem goes as follows: Determine all finite groups which have proper subgroups only of order 2 or 3.

Solution:

First off, let us observe that the cardinal of the required group G is of the form \(2^i3^j\). By the Sylow theorem, we will have a subgroup of order \(2^i\) and a subgroup of order \(3^j\). If both of them are positive and one is bigger than 2, then we will have a subgroup larger than order 2 or 3. Thus, G can only have \(2^k\), \(3^k\) or 6 elements.

In the first case, we get that all elements have order 2, and, thus, \(xy=yx\), for all elements of G. If this happens, we have a subgroup of order 4, made of \(x, y ,xy ,e\), so the only groups working in this case are Klein's group and the group of order 2, C2.

In the second case, we shall use the equation of the classes. Let us observe that, if 2 elements that aren't part of the same subgroup commute, then we shall have a group of order 9. By the equation of the classes, we have that \(3^k=|Z(G)|+Σ\frac{|G|}{|C(G)}\), where the sum is made by a complete system of representatives with non-trivial orbit.. Since \(C(G)<4\) by the observation above, it is easy to see that \(C(G)=3\), and, thus, if k is bigger than 2, we will need the center of G to have a number of elements that is a multiple of 3. Thus, we get that the only possible groups are the group of order 3 and the group of order 9. Thus, G is C3 or C9 or C3xC3.

In the third case, we have that G is either C6 or C3xC3.

This problem might not have been as easy as the Riemann Hypothesis, but it was fun nonetheless. Seriously though, it would be fun if someone actually proposed a correct solution of the actual RH on the first of April and someone disregarded it as a prank. Jokes aside, tune in next time for some stuff about complex numbers, another algebra problem, another Millennium Prize problem, or something completely random!

Cris.

Something similar to Fermat's Last Theorem on non-field finite rings

Finally, another post!

Today I shall discuss a problem from the National Maths Olympiad from 2000, the year I was born. Judging by the usual schedule of the Olympiad, this problem is probably my twin. It caught my eye because it literally disproves Fermat's Last Theorem on finite rings that are not fields (the title already said that). The FLT is, of course, a much harder problem than what I'm about to solve in the next few lines, but that doesn't make this problem less important.

Let (A,+,*) be a finite ring with 1 different from 0. Prove that the following affirmations are equivalent:
1. A is not a field.
2. The equation \(x^n+y^n=z^n\) has a solution for every natural n.

Solution:

We shall first prove that 2 implies 1. Let us presume by absurd that A is a field. Thus, since A is a field, (A\{0},*) is a finite group, with an order equal to a certain \(t\). For that \(t\), \(x^t=1\), for all elements of A\{0}. Thus, since the equation \(x^t+y^t=z^t\) has a solution, \(1+1=1\), so \(1=0\), which is false. Thus, A is not a field.

Conversely, if A is not a field, it means that it has a non-invertible element, let's call it \(x\). Since A is a finite ring, there are \(i<j\) such that \(x^i=x^j\), and, thus, \(x^i (x^{j-i}-1)=0\). By writing \(t=x^{i-1}(x^{j-1}-1)\), we have that \(x*t=t*x=0\). Now, let us take \((x+t)^n\). By the binomial theorem, this is a sum of combinations which revolve around \(x\) and \(t\), and, because \(x*t=t*x=0\), \((x+t)^n=x^n+t^n\), for all n, and, thus, we have a solution of the equation for every n.

Don't you think that this problem is really cute? I mean, it came 5 years after the proof of the FLT, and I am certain that the guy who proposed the problem had this in mind. I hope that my proof is correct, judging by the fact that the FLT has the unique record of having received the greatest amount of wrong solutions. Apparently, the peeps at the Wolfskehl committee received about 3 meters (in height) of wrong proofs. That might not sound like much, but when you think about the amount of pages required, you'll figure out that it's a really big lot. Tune in next time for trigonometric functions defined on complex numbers, another abstract algebra problem, or something completely random!

Cris. 

Two Problems from College Contests

MEME
REVIEW!!
Oh wait, wrong post.

I decided to start preparing for college contests by now, so I tried solving problems from such Maths contests. The first problem comes from the Imperial Mathematics Competition. At first, I didn't know how to solve it, and I told my good friend and classmate Dan about it. When he came up with a solution, I decided that I would solve it, too, and here's the proof I came up with. But first, the problem itself:

Let us presume that we use k>1 colors to color the lattice points of the plane. Is it true that there will always be a rectangle with vertices of the same color?

Solution:

Yes, it is true. In fact, the problem came as a two-parter: the first part of the problem asked you to prove this for k=2. Since this part proves the problem, I decided that I'd only discuss this one.

The proof is rather short, and I was surprised to see that. Due to the countability of the set of integer numbers, we can find, on a horizontal axis we shall call \(d_1\), an infinity of points of a certain color, \(c_1\). We shall now look on another axis, \(d_2\), but directly above the infinity of points of color \(c_1\). Since the infinity of points of color \(c_1\) is countable, with cardinal Aleph Null (I can't find the symbol for this one), we can take another infinity of points directly above these on \(d_2\) so that these new points have color \(c_2\). If \(c_2\) is the same as \(c_1\), then the problem is solved. Let us presume that they are different. If they are different, we can apply the same procedure for a certain \(c_3\) and \(d_3\), and, inductively, for a color \(c_{k+1}\) and \(d_{k+1}\). However, since there are only k colors, \(c_{k+1}\) will be the same as a certain \(c_i\), and, since the points on \(d_{k+1}\) are directly above those on \(d_i\), we will obtain an infinity of rectangles with vertices of the same color.

I found this proof rather interesting, because I was expecting it to be solvable by some sort of weird configuration when I first saw it. But this argument that I presented is way more beautiful, because it not only proves that there is one such rectangle, but rather proves that there is an infinity of such rectangles.

The second problem comes from the Traian Lalescu contest, the University-wide phase from the Universitatea Politehnica from Bucharest, and it's also in a Gazeta Matematica. One of my good friends who attended the contest showed me this problem, and I solved it using Taylor series. It was a bit tricky at parts, so I hope the solution is correct.

Let \(f:(0,\infty)->ℝ\) a derivable function and F one of its primitives. Prove that, if f' is bounded and \(\lim_{x\to\infty} F(x)=0\), then \(\lim_{x\to\infty} f(x)=0\).

Solution:

We shall prove this using Taylor series. For a certain \(x\) and a certain \(h\), we have that \(F(x+h)=F(x)+hf(x)+\frac {h^2}{2} f'(x)\). By taking \(x\) towards infinity, we get that \(\lim_{x\to\infty} hf(x)+\frac {h^2}{2}f'(x)=0\), so \(\lim_{x\to\infty} f(x)+\frac{h}{2}f'(x)=0\). This works for every h. Now we only have to deal with h, so we make it go towards 0. In order to prove that this method works (this is the part I'm not necessarily so sure about). Let us take \(h_n=\frac{1}{n}\). Since \(\lim_{x\to\infty} f(x)+\frac{1}{2n} f'(x)=0\), after a certain ε, every value of said function will be smaller in modulus than a certain Δ, so \(-Δ<f(x)+\frac{1}{2n}f'(x)<Δ\). But, we have that \(-M<f'(x)<M\), so \(-Δ<f(x)+\frac{1}{2n}M\), which implies that \(-Δ-\frac{1}{2n}M<f(x)<Δ+\frac{1}{2n}M\), by the same procedure. Since Δ and \(n\) can be taken as small as possible, we get, of course, that f tends to 0.

I wasn't really certain about the last part, that's why I wrote it with epsilon and delta. I believe that a simple commutation of limits would have been enough, but I wanted to make sure. 

Anyways, this has been it for today, folks. Tune in next time for either a complex number problem, an integral that I found on a shortlist, or something completely random!

Cris.

P.S: As you may know, I am a memer, and one of the greatest meme wars recently has been the Pewdiepie vs T-series war. It would be silly of me not to do my part, especially now, when the subscriber gap is getting smaller...

Inequality involving Lagrange Multipliers #2

Boy oh boy, the next installment in the epic saga of inequalities is finally here! How wonderful.

A while ago, one of my friends gave me this inequality, and, being the analysis enthusiast that I am, I couldn't resist using partial derivatives to solve it. Even though I found a solution, I feel a bit unfulfilled; I used Desmos to find the roots of a polynomial, and that wouldn't be allowed during a contest. Fortunately, this blog isn't a Maths contest, so it shall be allowed here. I suppose there were other methods of finding the roots of the polynomial I'm talking about, but they probably involved a lot of calculations that I wouldn't have had the patience to go through.

Let \(x,y,z\) be real, strictly positive numbers satisfying \(xyz=1\). Prove that \((x^{10}+y^{10}+z^{10})^2\) is bigger or equal to \(3(x^{13}+y^{13}+z^{13})\).

Solution:

Let \(f(x,y,z)=(x^{10}+y^{10}+z^{10})^2-3(x^{13}+y^{13}+z^{13})\) and \(g(x,y,z)=xyz\). We know that, in order to reach the extremes, $$∇f(x,y,z)=λ∇g(x,y,z) ⇒\frac{𝛛f}{𝛛x}=λ\frac{𝛛g}{𝛛x}$$The same relation works for \(y\) and \(z\). By differentiating, we get that $$20x^9(x^{10}+y^{10}+z^{10})-39x^{12}=λyz$$
$$⇒ 20x^{10}(x^{10}+y^{10}+z^{10})-39x^{13}=λ$$because \(xyz=1\). Thus, we get, by multiplying with \(y^{10}\), that $$20x^{10}y^{10}(x^{10}+y^{10}+z^{10})-39x^{13}y^{10}=λy^{10}$$
By doing the same for \(y\) and subtracting the two relations, we get that $$λ(y^{10}-x^{10})=39x^{10}y^{10}(y^3-x^3)$$and, by dividing the whole thing by \(x^{10}y^{10}\), which we can, since the numbers are strictly positive, we get that $$λ(x^{-10}-y^{-10})=39(y^3-x^3)$$This implies that $$λx^{-10}+39x^3=λy^{-10}+39y^3=λz^{-10}+39z^3$$since the relation is symmetrical. With that in mind, let \(h(x)=λx^{-10}+39x^3\). By differentiating this function, we get the derivative being equal to \(\frac {dh}{dx}=-10λx^{-11}+117x^2\).
Let us now prove that \(λ>0\). For this, we shall presume that \(x≤y≤z\), so that \(x≤1\), and look at \(20x^{10}(x^{10}+y^{10}+z^{10})-39x^{13}≥20x^{10}(x^{10}+2x^{-5})-39x^{13}=20x^{20}+40x^{5}-39x^{13}≥0\), with the first part coming from the AM-GM inequality and the second coming from the fact that \(x\) is smaller than 1. Thus, \(λ\) is positive.
Back to the derivative of \(h\), since \(λ\) is positive, we get that there is only one value of \(x\) for which the derivative is 0, and, thus, there are at most 2 points with the same output of the function. Thus, either \(x=y=z=1\), or \(x=y,z=x^{-2}\). In the latter case, we shall go back to \(\frac{𝛛f}{𝛛x}=λ\frac{𝛛g}{𝛛x}\) and \(\frac{𝛛f}{𝛛z}=λ\frac{𝛛g}{𝛛z}\) subtract the derivatives and multiply by \(x^{40}\) in order to obtain that \(40x^{60}-39x^{53}-20x^{30}+39x^{14}-20=0\). This is the part where I used Desmos.


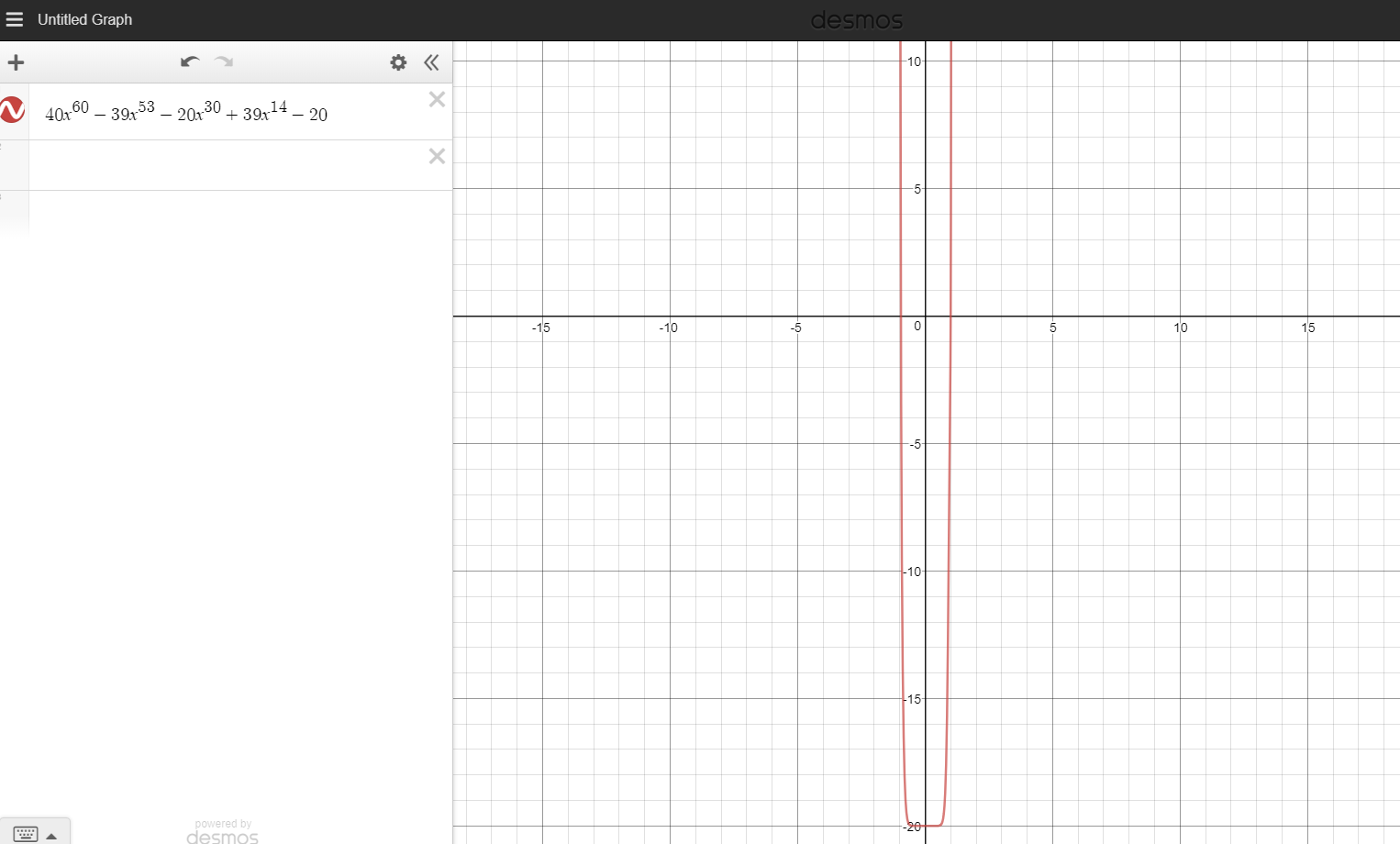
As you can see, the only real root of the polynomial is 1, so this means that \(x=y=z=1\) yet again. It's obvious that \(f(1,1,1)=0\), but now we have to prove that this is the minimal value, because we wanted to prove that \(f(x,y,z)≥0\) when \(g(x,y,z)=1\). Since this is a global extreme, we only have to find a triplet \(x,y,z\) for which the conditions apply. By taking \(z\) very large, towards infinity, and with \(x\) and \(y\) taken accordingly, we obtain an \(f\) that approaches infinity, and, thus, is bigger than 0. This concludes the proof.

Perhaps I should have tried finding the roots of that polynomial without computer help. I am not sure how I could have done it, but I asked one of the teachers at Oxford during the interview about that and he suggested a method of approximating the roots. Even so, calculating the roots without Desmos would have taken a really long while to write, and I am forever thankful to computers. I really liked this inequality, it really tests the solver's capacity of manipulating functions...and graphing applications. Tune in next time for a combinatorics problem taken from a college contest, or something completely random!

Cris.

Useful lemma about monoids and an application

It's a bit annoying to see the same thumbnail over and over on the front page of the blog, so I decided to change it a little bit. My apologies for the small text. I think I used the website hatchful for this one, while the other logo was made with logojoy.

Yesterday, while going through Olympiads, I found two problems that were eerily similar: one from the District Olympiad 2017 and one from the National Olympiad 2011. I shall solve the problem from 2011, while using the problem from 2017 as a lemma.

Let \((A,+,*)\) be a finite ring with the property that \(x^{n+1}+x=0\) has only two roots, 0 and 1. Prove that A is a field.

Solution:

First of all, let us note that, for \(x=1\), \(1+1=0\), so A has characteristic 2. Thus, the order of any element of \(x\) in the additive group \((A,+)\) is either 2 or 1, which implies that the cardinal of A, let's call it n, is a power of 2. Now, let us prove the following lemma:

Lemma:  Let (M,*) be a finite monoid and \(p\) be a natural number bigger than 2, such that \(a^p\) is different from \(a\), for every element \(a\) in M different than the identity element, \(e\). Prove that (M,*) is a group.

Proof: Let us consider such an \(a\). Since M is finite, there will be an \(i\) and a \(k\) , both natural numbers, such that \(a^i=a^{i+k}\). By continuously multiplying with \(k\), we get that \(a^i=a^{i+mk}\), for every \(m\). Thus, for every \(m\), by multiplying with \(a^{mk-i}\), we get that \(a^{mk}=a^{2mk}=a^{pmk}\), so \(a^{pmk}=a^{mk}\), and, thus, \(a^{mk}=e\), so \(a\) is invertible and (M,*) is a group.

Now it's time to apply the lemma to our problem. For any element \(x\) other than 1 and 0, \(x^{n+1}\) is different from \(-x=x\), because the characteristic is 2. By using the proof of the lemma on the monoid (A,*), we get two possibilities: either \(x^i=0\) or \(x^i=1\). All we have to prove now is that 0 is the only nilpotent element of the ring, because all the non-nilpotent elements are invertible.

If \(x\) is a nilpotent element, then let \(i\) be the rank of nilpotence. Thus, \(x^i=0\), while \(x^{i-1}\) is different than 0. By doing calculations, \((x^{i-1}+1)^{n+1}=x^{i-1}+1\) (keep in mind, n is a power of 2, and that is why the expansion is this. If n weren't a power of 2, the result wouldn't hold). Thus, \(x^{i-1}=1\) or \(x^{i-1}=0\), both contradicting the choice of \(x\), which leads to the fact that 0 is the only nilpotent element, which concludes the problem.

The monoid lemma is very useful in abstract algebra. I wonder who proposed the problems, since their similarity is very interesting. You can see, however, that the one from the NMO required a bit more thought, in order to prove that there's only one nilpotent element. Tune in next time, when I will finally post an inequality solved with Lagrange Multipliers. I already have it on paper, but partial derivatives are a bit harder to write than ring theory.

Cris.

Polynomials over a finite field

Oh well, here we go again. Back to Maths posts.

Tragedy struck since the last time we saw, my dear viewers. Oxford rejected me, but there's no time to waste, since the world of Maths is waiting. While going through National Olympiad shortlists, I found the following problem in the shortlist for 2013, randomly sitting at the middle of a page, waiting to be solved. It's a problem about polynomials, so I was surprised when I saw that I could solve it, because I'm not normally great at solving polynomial problems.

Let \(p>1\) be a prime, \((K, +, *)\) be a field with \(p^2\) elements and \(L=[0, 1, ... 1+1+...+1]\), with the last sum having \(p-1\) elements. Prove that for every \(x∊K-L\), there exists \(a,b∊L\) so that \(x^{2013}+ax+b=0\).

Solution:

I'm not sure if there are more ways of solving this particular problem, so for this you really need to have the idea.

Let us presume that there is an element \(x∊K-L\) such that \(x^{2013}+ax+b\) is always different than 0. The first observation is that have \(p^2-p\) elements in \(K-L\). Now, let \(A={(F(X)|F(X)=X^{2013}+aX+b}\). This set has cardinal \(p^2\). Since the cardinal of A is bigger than the cardinal of \(K-L\), we have that at least two polynomials from A have the same value in \(x\).

Let \(f_1\) and \(f_2\) be the associated polynomial functions of the polynomials we found. Thus, \(f_1(x)=f_2(x)\), so \(x^{2013}+a_1 x+ b_1=x^{2013}+a_2 x+ b_2\), so \((a_1 - a_2) x + (b_1 - b_2)=0\). Thus, \(x = (b_2 - b_1)(a_1-a_2)^{-1}∊L\), because \(a_1, a_2, b_1, b_2\) all belong to L and, because p is prime, L is closed under any operation. This contradicts the way we chose x, and thus the problem is solved.

The problem wasn't necessarily hard, but the idea was pretty important. This trick of finding two polynomial functions which have the same value in a point is widely used, though this is the first time I see it used in an abstract algebra problem. Tune in next time, when I might talk about inequalities and analysis, or something else, completely random.

Cris.