An interesting puzzle in probability (which has almost nothing to do with probability)

When I was younger, sometime during the 4th grade or so, I had this subject at school called 'Funny Mathematics' (quite informal for a school subject). I was quite intrigued by it during the summer before 4th grade, mainly because I had no idea what it would involve. I had high expectations from it, but was disappointed when the school year started and we got our manuals. After going through the 'Funny Mathematics' manual, I found out that it contained some sort of brain teasers ('If Mary's dad has 3 daughters, 2 of which are called May and August, what is the name of the 3rd one' and other variations of this question) and some puzzles with sticks (the typical 'move the sticks so that the resulting operation is correct' questions). Let me just say, I never found that type of Mathematics to be funny. However, earlier this year, I came across Martin Gardner's 'Colossal Book of Short Puzzles and Problems', which contained a lot of intriguing problems that reminded me that funny mathematics actually exists. One of them, proposed in the Probability chapter, goes as follows:

'A man arrives at a random spot several miles from the Pentagon. He looks at the building through binoculars. What is the probability that he will see three of its sides?'

The fact that he watches through binoculars implies that we don't have to deal with the limitation of eyesight; we can presume, for the sake of this problem, that the man can see the Pentagon from a point infinitely far from the Pentagon.

I will present two solutions, one trivial (the solution proposed in the book; sadly, I didn't think of it), and my solution, involving calculus.



First solution:

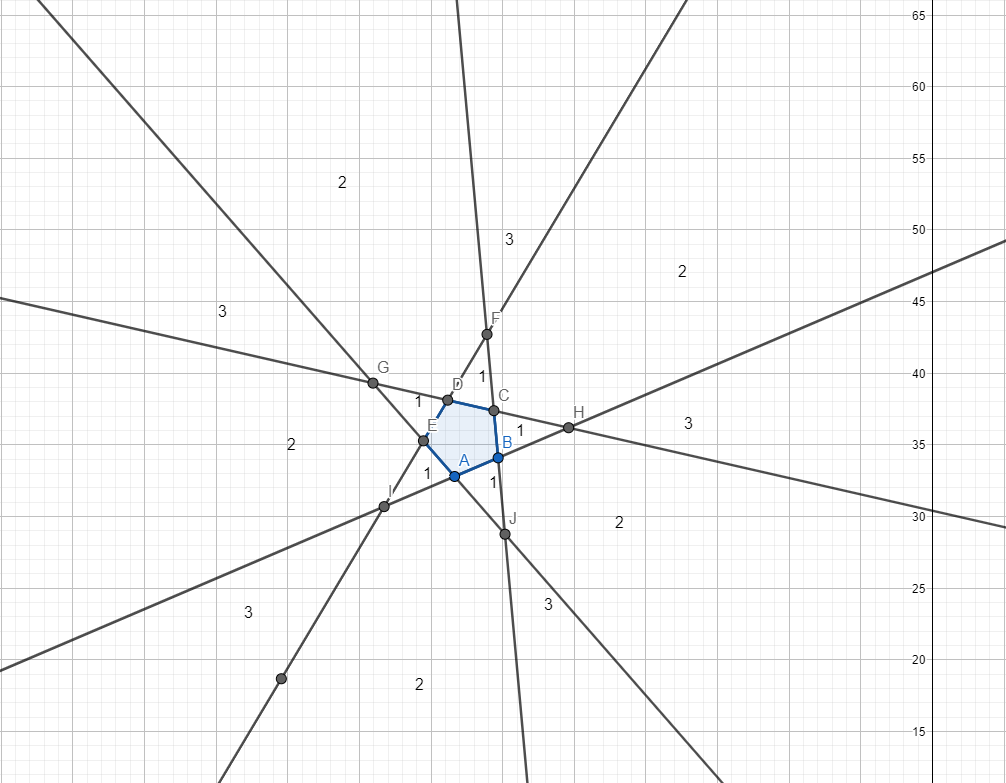
Let us drawn the Pentagon and call it ABCDE. By intersecting the sides of the Pentagon, we can denote the areas in which the observer can see 1, 2 or 3 sides.

The drawing above shows the areas for which the observer sees 1, 2 and, respectively, 3 faces of the pentagon. Let us observe that, if the observer stays in a 2-area, then the symmetric of the observer through the center of the Pentagon, then the symmetric of the observer has an infinitely small chance of lying in the 1-area and a probability of being in a 3-area. Thus, the probability of the observer seeing 3 sides is the same as the probability of the observer seeing 2 sides, and the probability that the observer sees 1 side tends towards 0. Thus, \(P(1)+P(2)+P(3)=2P(3)=1\), so \(P(3)=1/2\).

Sadly, as I said, I couldn't see this solution when I solved the problem. Let me show you my solution.

Second solution:



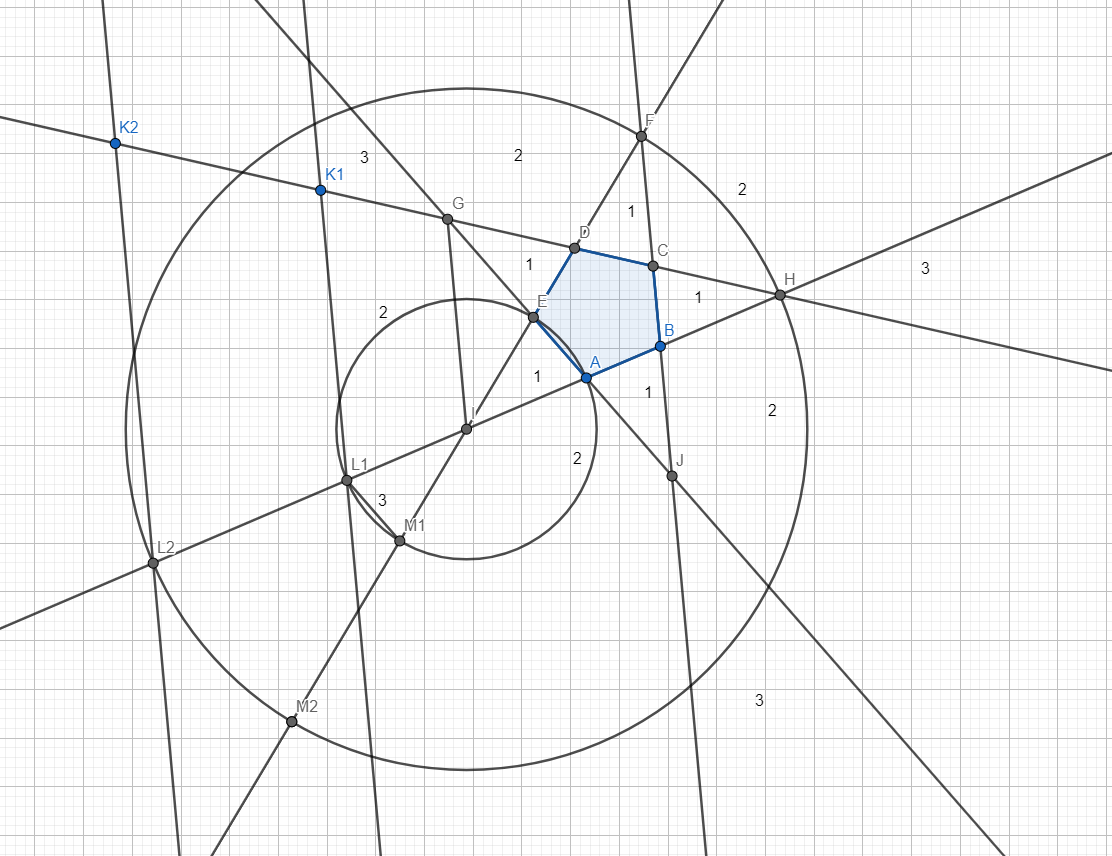
We shall keep the notations we used during the last solution. Since all the 2-areas and 3-areas are the same, we shall only look at one pair of such areas: The 3-area denoted by ED and AB, and the 2 area denoted by DC and AB. On the line DC, let us take the point $K_1$. Let \(L_1\) be the intersection of the line parallel to GI drawn through \(K_1\), and let \(M_1\) be a point on ED such that \(IL_1=IM_1\). Obviously, \(GIL_{1}K_{1}\) is an isosceles trapezium. Let \(x=GK_1\). The area of the trapezium \(GIL_{1}K_{1}\) is

\(A_{1}(x)=((GI+K_{1}L{1})/2)*h_{1}(x)\).

Since ABCDE is a regular pentagon, its angles are all equal to 108 degrees. After doing some angle chasing, we can deduce that the angles in \(GIL_{1}K_{1}\) are 108 degrees and 72 degrees.

$$K_{1}L_{1}=GI+2x*cos(18)$$

Thus,

$$A_{1}(x)=((2GI+2x*sin(18))/2)*(x cos(18))$$
$$=GI*xcos(18)+x^{2}*(sin(36)/2)$$

, and the area of \(IL_{1}M_{1}\), which is \(A_{2}(x)\), is equal to

$$A_{2}(x)=(x^{2}*sin(36))/2$$

Thus, $$[A_{1}(x))/(A_{2}(x)] = [GI*xcos(18)+x^{2}*(sin(36)/2)]/[x^{2}*(sin(36)/2)]$$. It is easy to observe that

$$\lim_{x\rightarrow infinity}\ (A_{1}(x)/A_{2}(x))=1$$, and, thus, the probability that the observer sees 3 sides is the limit towards infinity of \((A_{1})/(A_{1}+A_{2}+C)\), where C is the constant sum of the 1-areas and the small triangles in the 2-areas that weren't part of \(A_{2}(x)\).

This problem was really interesting to solve, and I pretty much enjoyed the fact that it could be solved through calculus. I am a geometry enthusiast, and combining geometry with ANYTHING else is amazing. 

Ion Barbu, one of the great Romanian intellectuals (he was both a Mathematician and a Poet), once said that, and I quote, 'as contradictory as these subjects might be at first sight, there is, somewhere, in the higher planes of geometry, a place where it meets poetry.' I tend to agree with him, to be honest. I believe that the higher planes of geometry (I love this expression, it's kind of pun-y) intersect with many other fields of study, which I am eager to explore.

Cris.