Matrix solvable through Jordan form

One of the worst experiences (and failures) of my life was the National Maths Olympiad from the 11th grade. It was a traumatizing experience, since the Olympiad took place in a remote part of the country (I come from Romania), and the subjects were incredibly hard. I managed to win a bronze medal, though I was very disappointed with myself. A month ago, I gathered my strength and looked through the shortlist for the Olympiad. The problem I am about to solve was the only linear algebra problem in the shortlist, and, just like the one from the Olympiad, it is solvable through the Jordan canonical form. The Jordan form wasn't part of the syllabus of the Olympiad, which was a dirty move from the problem selection committee. Nonetheless, I was inspired by this experience, and, in the meantime, I studied the canonical form.

Without further ado, let's get straight into the problem.

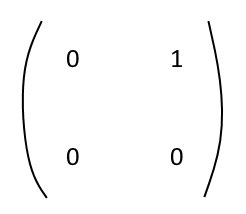
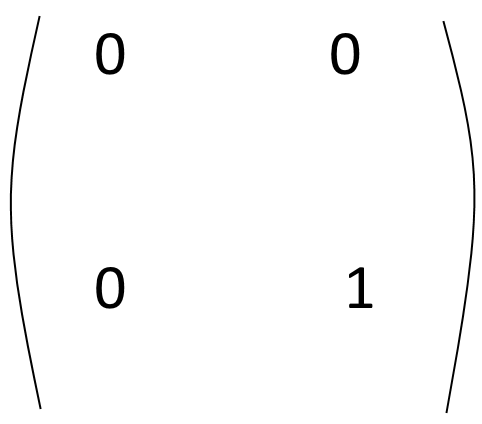
Let A be an \(n x n\) matrix with complex entries. Prove that \(A^2=O_{n}\) if and only if there are complex \(n x n\) matrices B and C such that \(A = BC\) and \(CB=O_{n}\).

I will post the matrices as photos, because posting them in Latex is tedious.

Let 1) be \(A^2=O_{n} => B, C\), and 2) be \(B, C => A^2=O_{n}\).

2) => 1)

$$A=BC, CB=O_{n}$$

$$A^2=B(CB)C=O_{n}$$

The next one will be 'slightly' longer.

1) => 2)

\(A^2=O_{n}\) Thus, the minimal polynomial of A divides \(X^2\).

1. The minimal polynomial of A is X, so \(A=O_{n}, B=O_{n}\), while C is any random matrix.

2. The minimal polynomial is \(X^2\)

We shall start using the Jordan canonical form. We know that the maximum order of any Jordan block corresponding to a specific eigenvalue is equal to the number of apparitions of \(X-a\) (where a is an eigenvalue) in the minimal polynomial. Thus, the maximum order of a Jordan cell is 2, and the Jordan canonical form of A looks something like this:

Everything above the J-s and 0-s is 0. The J-s look something like this:

We shall be looking for matrices B' and C' such that \(B' C' = J\) and \(C' B' = O_{n}\)

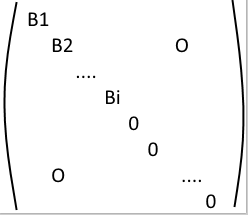
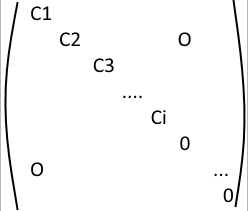
Let us write B' and C' in the form

   , .

We need to find \(B_{i}\) and \(C_{i}\) such that \(B_{i} C_{i} = J_{i}\) and $$C_{i} B_{i} = O_{n}$$. The perfect example of such matrices is \(B_{i}=J_{i}\) and \(C_{i}\) of the form

With \(B_{i}\) and \(C_{i}\) found, we can write B' and C'. 

Let S be a matrix such that \(SAS^{-1} = J\). Thus, \(S^{-1}JS=A\), and \(S^{-1}B' C' S=A\). We can take \(B=S^{-1}B'\), and \(C=C'S\). Thus, \(BC=A\) and \(CB=C'SS^{-1}B'=C'B'=O_{n}\), so there exist B and C, which concludes the problem.

It was very interesting to solve a problem with the Jordan canonical form, as the methods used aren't very common in high school Mathematics. The problem itself wasn't extremely difficult, yet it was interesting nonetheless. Tune in next time for an article that might be about something rather...different.

Cris.