An application of Complex Algebra in Geometry

A few days ago, I wrote about posting my favorite problem. The thing about this problem is that it's extremely simple through synthetic geometry, but I found a way of solving it using complex numbers in a way that baffled me. It took 3 pages to solve this problem in my 'Notebook of Nice Problems' (which we shall call NNP from now on; I might even add a tag for problems I took from there). Some people have called me sadistic for liking this type of solutions, but I took it as a compliment. Without further ado, let's get right into the problem!

Let ABC be a triangle with AD as a bisector and AM as a median, with D and M laying on the line BC. Let P be a random point on AD, and E and F the projections of P on the lines AB and AC. If K is the intersection between EF and AM, prove that PK is perpendicular on BC.



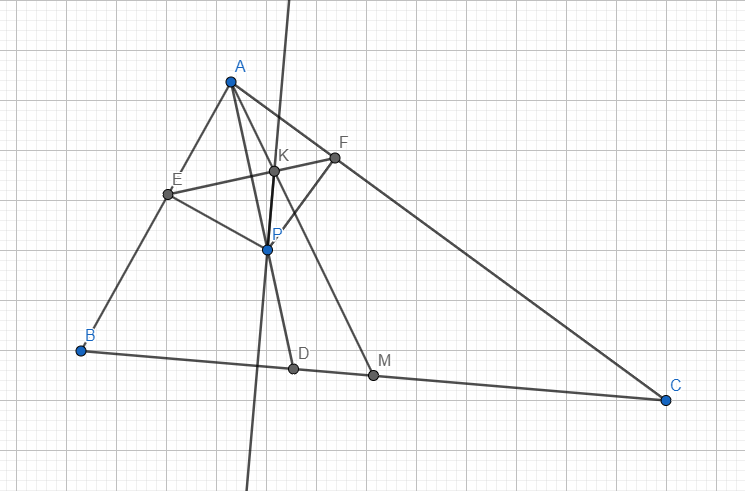
First of all, we shall presume that ABC is not isosceles with AB=AC. If ABC is isosceles with AB=AC, then AD and AM coincide, and PK is obviously perpendicular on DC.

Let us use the transversal theorem in the triangle ABC. We shall consider the transversal E-K-F, and the line denoted by A-K-M, which passes through K. Thus, we get that $$BM \frac{FC}{FA} + MC \frac{EB}{EA} = BC \frac{KM}{KA}$$However, \(AM=MC=\frac{BC}{2}\), so we get that $$\frac{FC}{FA}+\frac{EB}{EA}=2\frac{KM}{KA}$$We shall call this relation (1). By using the property of points on the bisector, we get that \(PE=PF\), and, by triangle congruences, \(AE=AF\). Thus, (1) transforms into \( \frac{FC+EB}{2EA}=\frac{KM}{KA}\). However, \(FC=AC-AF\), and \(EB=AB-AE\), so the relation transforms further into \( \frac{AB+AC}{2EA} -1=\frac{KM}{KA}=r\).

Let us center the complex plane in A. By using the usual notations and by considering AB as the real positive axis, we have that \(e,b⋲R_{+}^*\). We can write \(k=\frac{m+r*a}{1+r}=\frac{m}{1+r}=\frac{b+c}{2(1+r)}\) (2)

Since \( PE⟘AB, PF⟘AC, PE=PF\), it follows that \(\frac{e-p}{b}⋲iR, \frac{f-p}{c}⋲iR, |e-p|=|f-p|\). $$\frac{e-p}{b}⋲iR ⟺ \frac{e-p}{b}=\frac{p^{*}-e^{*}}{b^{*}},$$where \(x^{*}\) is the conjugate of \(x\). $$⟹eb^{*}+e^{*}b=pb^{*}+p^{*}b$$
Similarly, we get that $$fc^{*}+f^{*}c=pc^{*}+p^{*}c$$We shall call these relations (3) and (4) respectively. Apologies for not being able to write the relations next to the equations, I still have to work on my Mathjax skills. I will (probably) learn how to fix this problem in the (far) future. If \(w=cosA+isinA ⟹ f=ew\). \(PK⟘BC ⟺\frac{k-p}{c-b}=\frac{p^{*}-k^{*}}{c^{*}-b^{*}}\).
$$⟺kc^{*}-pc^{*}-kb^{*}+pb^{*}=p^{*}c-ck^{*}-p^{*}b+bk^{*}$$
$$⟺kc^{*}+k^{*}c-bk^{*}-b^{*}k=p^{*}c+c^{*}p-p^{*}b-pb^{*}$$
$$⟺kc^{*}+k^{*}c-k^{*}b-kb^{*}=fc^{*}+f^{*}c-eb^{*}-e^{*}b$$The last line is obtained from combining (3) and (4), and we shall call it (5). Let us replace k as we obtained it in (2). Let us also remember that e and b are positive numbers, so they are equal to their conjugate and modulus.

$$⟹ (5) ⟺ \frac{(b+c)c^{*}}{2(1+r)}+\frac{(b^{*}+c^{*})c}{2(1+r)}-$$
$$-\frac{(b^{*}+c^{*})b}{2(1+r)}-\frac{(b+c)b^{*}}{2(1+r)}=ewc^{*}+ew^{*}c-eb^{*}-e^{*}b$$
$$⟺\frac{|c|^2-|b|^2|}{1+r}=ewc^{*}+ew^{*}c-eb-e^{*}b,$$which shall be known from now on as (6). Let us remember that \(\frac{AB+AC}{2EA}=1+r ⟹\frac{|b|+|c|}{2|e|}=1+r.\)
$$⟹ (6) ⟺ \frac{2e(|c|-|b|)(|c|+|b|)}{|b|+|c|}=ewc^{*}+ew^{*}c-eb-e^{*}b$$
$$⟺ 2(|c|-|b|)=cw^{*}+w^{*}c-2b$$
This shall be known as (7). However, \(c=\frac{w|c|b}{|b|}\).
$$⟹(7)⟺2(|c|-|b|)=ww^{*}b^{*}\frac{|c|}{|b|}+ww^{*}b\frac{|c|}{|b|}-2b$$
$$⟺2(|c|-|b|)=2b\frac{|c|-|b|}{|b|} ⟺ 2=2$$
The last line is true, because |c| is different than |b|, as AB is different than AC. Thus, \(PK⟘BC\) 𞺑

Writing that square at the end of this proof feels so satisfying. The calculations were very tedious when I first solved the problem, but I enjoyed it nonetheless. Of course, in the actual context of Mathematics, this proof isn't hard, but it's a nice exercise for anyone with basic knowledge of complex numbers and with a bit of imagination regarding Geometry.

P.S: This will be the last template update for a while, as I pretty much like this layout of the blog.

Cris.

Property of real skew symmetric matrices

If you don't know what a skew-symmetric matrix is, don't worry; I didn't know what it meant either until I found this problem. It's literally a matrix A for which \(A^T=-A\). In this article, we have to prove that the rank of any real skew symmetric matrix is even. From what I've been told, the rank of any skew symmetric matrix, in any field with characteristic different than 2, is even, but for now I only know how to prove this property for the \(M_n {(R)}\). Without further ado, let's get straight into the problem.

First of all, let us prove a few lemmas:

1. If A is a real skew symmetric matrix, then it is diagonalizable.

Through Schur's theorem, we see that there is a matrix \(S\) in \(M_n (R)\) that satisfies the following properties: \(SS^{T} = I_n\) and \(SAS^{-1} = J\), where J is an upper triangular matrix. By writing \(S^{-1}=S^{T}\) and the same relation with S, we have that \(-(S^{-1})^{T}A^{T}S^{T}=-J^{T}\), and \(J^{T}\) is a lower triangular matrix. J is a diagonal matrix, because the entries under the diagonal, 0s, are equal to the negatives of the values above the diagonal. Thus, A is diagonalizable.

2. The eigenvalues of a real skew symmetric matrix are either pairs of complex conjugates or 0.

If \(\lambda\) is an eigenvalue of A, then \(AX=\lambda X\), for a certain vector X. By transposing, we get that \(X^{T}A^{T}=\lambda X^{T}\). Conjugate the whole thing, then multiply to the right by \(X\) and replace \(A^{T} = -A\) and \(AX=\lambda X\), and you get that \(\lambda\) is a purely imaginary number or 0. In order to prove that the conjugates are eigenvalues too, we just look at the characteristic polynomial of A is \(\lambda\), and conjugate it. Since A is real, it's characteristic polynomial has real coefficients, so the conjugate of \(\lambda\) is also a root.

Now we are ready to solve the problem. Since A is diagonalizable, then there exists an S such that \(SAS^{-1}=J\), where J is the Jordan canonical form of A. Since the eigenvalues of A come in pairs of conjugates, the rank of A is equal to 2 times the number of non-zero eigenvalues, so it is even.

As with most matrix problems that use this theory, they are somewhere on the boundary between college Mathematics and high school Mathematics. As far as I know, the high school curriculum doesn't include Jordan forms or Schur's theorem in any country (perhaps except for some countries in Asia). Apologies for the fact that this article is a bit smaller, but I've got something really interesting on the way; one of my all time favorite problems is coming in the next article.

Cris.

Benford's Generalized Law

First of all, apologies for my lack of posts recently; school started for me, so I don't really have time for much. I have been working on an article regarding the Hollow Earth theory in which I debunked it, but, after writing the article, I realized that I made a mistake somewhere along the way, and, frankly speaking, I rage-quited. I still wanted to write an article, so I took out my 'notebook with notable problems' (I have one of those, I'm a full-time nerd), and I came across the Newcomb-Benford law, which states that the numerical values of the vast majority of social phenomena (the majority modeled by exponential evolutions in rapport to time) start with 1. The law takes its name from its two discoverers, Frank Benford, who wrote about it in 1938, and Simon Newcomb, who discovered it in 1881. Both discovered it independently from one another.  This problem was also proposed in a Gazeta Matematica back in February 2017.

Let \(f(t)=a^t\) be the function modeling a specific social event. We are looking at the values of t for which $$10^n<f(t)<2*10^n$$. By taking logarithms, we get that \( n<t log(a)<lg2 + n\). Thus, the probability that the first digit of f is 1 is log2, which is roughly equal to 0.301. For the general case, $$lg(d)+n<t lg(a)<lg(d+1)+n$$,where d is the first digit of f, so the probability that the first digit is d is equal to \(log(d+1)-log(d)\). The function \(log(x+1)-log(x)\) is decreasing for all positive x, so the probability of each digit appearing is decreasing. Obviously, the law works for all numerical bases.

We can also do a quick generalization of this result. How about we derive the n-th digit of an exponential function? Let us presume that the exponential function has m digits, with m bigger than n. Now, we know that \((10M+d)*10^{m+1-n}<a^t<(10M+d+1)*10^{m+1-n}\), where M is the number composed by the first n-1 digits. Thus, by taking logs again, we get that $$(m+1-n)log(10M+d)<tloga<(m+1-n)log(10M+d+1)$$, so the required probability, for a certain M, is \(log(1+ \frac {1}{10M+d})\). Since M is the number made by the first n-1 digits, it takes values from \( 10^{n-2}\) to \(10^{n-1}-1\), so the required probability is $$P(d)= \sum_{k=10^{n-2}}^{10^{n-1}-1} log(1+ \frac {1}{10k+d})$$.

After doing a quick search on Wikipedia, I found out that this result has some practical uses. Apparently, price digits and election results can be somehow checked by this law, and it appears to have applications in molecular genetics, too. Perhaps some old results like this are still revolutionary to this day.

Cris.

Making a tour of a square grid

The new design update of the blog deserves a content update too, don't you think? This problem is part of the 'Intriguing Puzzles' series, which I will post from time to time.

This specific puzzle is rather well known, and I am sure that most people may recognize this. There are lots of puzzles regarding 'tours' of certain buildings; by tour, I mean going through each room only once and then returning to the starting room. There is a problem, however: not all buildings can be toured. For this puzzle, we will consider a nxn rectangular grid. Let us look at a 5x5 grid.

We shall prove that such rectangular grids can't be toured. I came across this problem in the Oxford Mathematics Aptitude Test from 2009, yet I am sure that it was posed many times before.

By absurd, we shall presume that the grid can be toured.

Let us color the rectangular grid in black and white like a chessboard:



A 'move' is defined as the movement from one room to a neighboring room. Let us observe that, if a tour starts in a room of a certain color, it takes an even number of moves to return to a room of the same color. A tour of a grid should consist as \(n^2\) moves, as that's the number of rooms you need to tour. In the case of an odd n, the number of rooms is odd, so the number of moves is odd. Thus, after \(n^2\) moves, you can't return to a room of the same color as that of the room you started from, resulting in a contradiction.

The problem given by Oxford was more complicated than this; this was the last part of the problem given at Oxford. In the first four parts, you had to deal with a rectangular \(n*n\) grid with an even n. This problem reminds me of a puzzle regarding covering a chessboard with dominoes because of the strategy used. But that's a puzzle for another time.

Cris.

Solar System's Escape Velocity

This is a step-up from the previous post about the Earth's escape velocity, though this one won't be as exact as the one before. The Solar System is a lot more complicated than what I am about to do, but it's a pretty nice challenge for anyone interested in problems regarding gravity. We shall consider the problem as it was asked by Thomas Povey in his 'Professor Povey's Perplexing Problems' book: only the Sun and Earth affect the escape velocity. Let us calculate the escape velocity from the Solar System, in the reference frame of the Earth's surface. Let \(\alpha\) be the angle at which a probe is sent outside of the Solar System.

First off, a few conventions: the distance between the Sun and the Earth is 149.6 million kilometers, the radius of the sun is 695,508 kilometers, the mass of the sun is \(2*10^{30}\) kilograms, the mass of the Earth is \(6*10^{24}\) kilograms, and the radius of the Earth is 6,371 kilograms, and the gravitational constant G is \(6.6*10^{-11} \frac {N m^2}{kg^2}\).

Let's take a look at the following drawing:



Let S be the center of the Sun, E the center of the Earth. Let the vector CD be the direction our probe is sent outside the Solar System. In order to find the required speed, we first need to find the speed at which the Earth rotates around its own axis, and the speed at which the Earth rotates around the Sun.

$$V_E=W_E R_E$$, where \(W_E\) is the angular velocity of the Earth around its own axis. We know the frequency at which the Earth rotates, the inverse of the number of seconds in a day, \(\frac {1}{86400}\) seconds. Thus, \(W_E = \frac {2\pi}{86400} rad*s^{-1}\). Through an easy calculation, we get that \(V_E=0.47 \frac {km}{s}\).

Now for the speed around the Sun. The frequency of a rotation is \(\frac {1}{86400*365}=\frac {1}{31536000}\). The speed at which the Earth rotates around the sun is \(V_{ES}=W_{ES}R_{ES}\), which is approximately \(30 \frac {m}{s}\).

The next part of the question is to figure out the work required to leave the Solar System. This work is equal to the sum of the work required to escape the Earth and the work required to escape the Sun. Thus, this work is $$W=\int_{R_E}^{\infty} \frac {G M_E m}{r^2} dr + \int_{R_{ES}}^{\infty} \frac {G M_{ES} m}{r^2} dr = \frac {GM_E m}{R_E} + \frac {GM_S m}{R_{ES}}$$. This work must be equal to the kinetic energy, so $$ \frac {GM_E m}{R_E} + \frac {GM_S m}{R_{ES}} = \frac {mv^2}{2}$$

Thus, $$v=\sqrt{2G(\frac {M_E}{R_E} + \frac{M_{S}}{R_{ES}})}=43.67 \frac {m}{s}$$.

Let \(v_i = V_{ES}+V_E = 30.47 \frac {km}{s}\). This is the modulus of the vector \(\vec{CD}\). The escape velocity is the modulus of the difference between the vectors \(\vec{EB}\) and \(\vec{CD}\), where the modulus of EB is \(v\). Let us decompose \(\vec{v_i}\) on the \(O_x\) and \(O_y\) axis. \(\vec{v_i} = v_i cos(\alpha) \vec{i} + v_i sin(\alpha) \vec{j}\). Thus, the required speed is $$v_{esc}=|\vec{v}-\vec{v_i}|=\sqrt {(v - v_i cos(\alpha))^2 + (-v_i sin(\alpha))^2}=$$
$$=\sqrt { v^2-2v*v_i sin (\alpha) +(v_i)^2}$$.

As a small observation, the smallest escape speed is when \(\alpha = \frac {\pi}{2}\), which is equal to roughly 13.2 kilometers per second, while the largest escape speed is when \(\alpha=- \frac{\pi}{2}\), and is roughly equal to 74.2 kilometers per second. The direction is highly important when launching satellites, as can be seen by the given calculations.

It would be fun to find the escape velocity of the Galaxy as the generalization. I did a quick research, and, apparently, the escape velocity of the Galaxy is 537 kilometers per second. That's about 2,073,600 kilometers per hour. For comparison, the fastest man-made object ever is the spacecraft Helios 2, which, in 1989, was moving away from the Earth at a speed of 356,040 kilometers per hour. It's going to take a long while before we leave the Galaxy.

Cris.

Nice Step 2 Probability Question

As you may have noticed, I am an enthusiast of anything mathematical. Applying mathematics in something from the natural world is a pretty intriguing idea to me, even though I haven't really studied Physics as much as I should have during high school. The closest I can come to something 'real' by doing Maths is through Probability questions. While most questions revolve around random variables and probabilities regarding those, there are some questions which revolve around easy-to-understand events. Here's one of those problems, which I found in the 2011 Step 2 (one of the exams needed to get admitted to Cambridge).

Xavier and Younis (pretty weird names) are playing a match. The match consists of a series of games and each game consists of three points. Xavier has probability p and Younis has probability 1-p of winning the first point of any game. In the second and third points of each game, the player who won the previous point has probability p and the player who lost the previous point has probability 1-p of winning the point. If a player wins two consecutive points in a single game, the match ends and that player has won; otherwise,the match continues with another game.

a) Let w be the probability that Younis wins the match. Show that for p different than 0, $$w=\frac {1-p^2}{2-p}$$. Show that \(w>1/2\) if \(p<1/2\), and \(w<1/2\) if \(p>1/2\). Does w increase whenever p decreases?

This is the longest part of the problem. Let us analyze what happens during each game through a probability tree.


In the image above, Y stands for Younis winning a point and X stands for Xavier winning a point. It is easy to say that the probability of  Younis winning is $$p-p^2+p(p-p^2)=p-p^3$$. The probability of neither winning nor losing is $$(1-p)^3+p(1-p)^2=(1-p)^2$$.

The probability of Younis winning the first game is the probability above, \(p-p^3\). For Younis to win in the second match, the first match must conclude in a draw, and, thus, the probability of Younis winning in the second match \((1-p)^2 (p-p^3)\). Thus, the probability of Younis winning is an infinite sum: $$w=(p-p^3)\sum_{n=1}^{\infty}(1-p)^{2n}=\frac {1-p^2}{2-p}$$

By differentiating in rapport to p, \(\frac {dw}{dp} = \frac {p^2-4p+1}{(2-p)^2}\), which is bigger than 0 if \(p^2-4p+1>0\), which happens if p isn't in the interval between \(2-3^{1/2}\)and \(2+3^{1/2}\). Since the first fraction is smaller than 0.5 and the latter is bigger than 0.5, it means that \(w\)is decreasing in 0.5, and \(w(0.5)=0.5\), so the conclusion of the problem holds.

b) If Xavier wins the match, Younis gives him 1 pound; if Younis wins the match, Xavier gives him k pounds. Find the value of k for which the game is 'fair' in the case when p=2/3.

It is easy to say that Younis' expected profit is \(w\) pounds, while Xavier's expected profit is \((1-w)k\). $$w(2/3)=\frac {5}{12}, (1-w)k=\frac {7}{12}k=\frac {5}{12}$$, so \(k=\frac {5}{7}\)pounds.

c) What happens if \(p=0\)?

If \(p=0\), then Younis will win the first and last points in each game, and Xavier will win the second point; thus, the game never ends, as no one will win two consecutive games.

It is pretty hard to come across elementary Probability problems, even in undergraduate exam papers. I pretty much enjoy this type of problems, as it challenges the student to think about a (more or less) real situation and apply probability in it. This problem was rather easy, yet it was pretty fun to solve, at least for me. Tune in next time for who-knows-what type of problem.

Cris.